题目内容
已知f(x)=x2-2x,则满足条件
的点(x,y)所形成区域的面积为______.
|
∵f(x)=x2-2x
∴约束条件
|
可以转化为
|
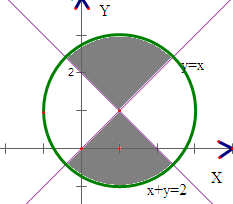
其对应的可行域如下图示:
其面积为:
| 1 |
| 2 |
| 2 |
故答案为:π

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
题目内容
|

|
|
| 1 |
| 2 |
| 2 |

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案