题目内容
 如图所示,圆O上一点C在直径AB上的射影为D,CD=4,BD=8,则AD的长等于( )
如图所示,圆O上一点C在直径AB上的射影为D,CD=4,BD=8,则AD的长等于( )分析:直径所对的圆周角为直角,所以在Rt△ABC中CD是斜边AB上的高,可得△ADC∽△CDB,得到比例线段AD:DC=DC:DB,从而得到CD是AD、BD的比例中项,可算出AB的长.
解答:解:∵AB是圆O的直径
∴AC⊥BC
∴∠B+∠A=90°
∵CD⊥AB
∴∠B+∠DCB=90°
∴∠DCB=∠A
∴Rt△ADC∽Rt△CDB
∴
=
⇒DC2=AD•DB
∵CD=4,BD=8
∴AD=
=2
故选A
∴AC⊥BC
∴∠B+∠A=90°
∵CD⊥AB
∴∠B+∠DCB=90°
∴∠DCB=∠A
∴Rt△ADC∽Rt△CDB
∴
| AD |
| DC |
| DC |
| DB |
∵CD=4,BD=8
∴AD=
| DC 2 |
| BD |
故选A
点评:本题以圆中的直角三角形为例,考查了直角三角形的射影定理,属于基础题.找到题中的相似三角形,利用比例线段求长度,是此类问题的常用方法.

练习册系列答案
相关题目
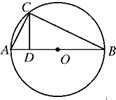 如图所示,圆O上一点C在直径AB上的射影为D,CD=4,BD=8,则圆O的半径等于
如图所示,圆O上一点C在直径AB上的射影为D,CD=4,BD=8,则圆O的半径等于 A(不等式选做题)若x>0,y>0且x+2y=1,则
A(不等式选做题)若x>0,y>0且x+2y=1,则 (2013•东莞一模)(几何证明选讲选做题)
(2013•东莞一模)(几何证明选讲选做题) 