题目内容
13.已知函数f(x)=$\left\{\begin{array}{l}{(2x-{x}^{2}){e}^{x},x≤0}\\{-{x}^{2}+4x+3,x>0}\end{array}\right.$,g(x)=f(x)-3k,若函数g(x)恰有两个不同的零点,则实数k的取值范围为(1,$\frac{7}{3}$)∪{0,$-\frac{2\sqrt{2}+2}{3{e}^{\sqrt{2}}}$}.分析 由g(x)=0,利用方程和函数之间的关系,转化为求函数f(x)的极值问题,利用数形结合即可得到结论.
解答 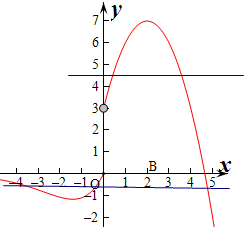 解:由g(x)=f(x)-3k=0,即f(x)=3k,
解:由g(x)=f(x)-3k=0,即f(x)=3k,
当x≤0时,f(x)=(2x-x2)ex,
则f'(x)=(2-x2)ex,由f'(x)=(2-x2)ex=0,解得x=-$\sqrt{2}$,
当x=-$\sqrt{2}$时,函数f(x)取得极小值f(-$\sqrt{2}$)=$(-2\sqrt{2}-2{)e}^{-\sqrt{2}}$,
当x>0时,f(x)=-x2+4x+3=-(x-2)2+7≤7,
作出函数f(x)的图象,由图象可知,要使f(x)=3k有恰有两个不同的交点,
则满足3<3k<7或$(-2\sqrt{2}-2{)e}^{-\sqrt{2}}$=3k或k=0,
即1<k<$\frac{7}{3}$或k=$-\frac{2\sqrt{2}+2}{3{e}^{\sqrt{2}}}$或k=0,
故答案为:(1,$\frac{7}{3}$)∪{0,$-\frac{2\sqrt{2}+2}{3{e}^{\sqrt{2}}}$}
点评 本题主要考查函数零点个数的判定,将方程转化为两个函数的相交个数问题是解决本题问题的基本方法.利用导数研究函数f(x)的极值是解决本题的关键.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
18.若(3x-1)7=a7x7+a6x6+…+a1x+a0,则a1+a3+a5+a7=( )
| A. | 26-213 | B. | 26+213 | C. | 27-214 | D. | 27+214 |
 如图,△ABC为直角三角形,∠ABC=90°,以AB为直径的圆交AC与点E,点D是BC边的中点,连接OD交圆于点M,求证:
如图,△ABC为直角三角形,∠ABC=90°,以AB为直径的圆交AC与点E,点D是BC边的中点,连接OD交圆于点M,求证: 如图,已知$\overrightarrow{OP}$=(2,1),$\overrightarrow{OA}$=(1,7),$\overrightarrow{OB}$=(5,1),设Z是直线OP上的一动点.
如图,已知$\overrightarrow{OP}$=(2,1),$\overrightarrow{OA}$=(1,7),$\overrightarrow{OB}$=(5,1),设Z是直线OP上的一动点.