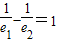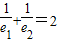题目内容
已知椭圆 与双曲线
与双曲线 共焦点,点P是该椭圆与双曲线在第一象限的公共点,如果以椭圆的右焦点为焦点,以y轴为准线的抛物线恰过P点,那么椭圆的离心率e1与双曲线的离心率e2之间的关系为
共焦点,点P是该椭圆与双曲线在第一象限的公共点,如果以椭圆的右焦点为焦点,以y轴为准线的抛物线恰过P点,那么椭圆的离心率e1与双曲线的离心率e2之间的关系为
- A.e2-e1=1
- B.e1+e2=2
- C.

- D.

A
分析:设椭圆及双曲线的半焦距为c,左右焦点分别为F1、F2,P点的坐标为(x,y).根据圆锥曲线的共同定义,则对于椭圆而言:PF1=a1+e1x,PF2=a1-e1x,对于双曲线而言:PF1=e2x+a2,PF2=e2x-a2,对于抛物线而言:PF2=x,从而建立a1-e1x=e2x-a2=x,消去x化简即得答案.
解答:设椭圆及双曲线的半焦距为c,左右焦点分别为F1、F2,P点的坐标为(x,y).
则对于椭圆而言:PF1=a1+e1x,PF2=a1-e1x,
对于双曲线而言:PF1=e2x+a2,PF2=e2x-a2,
对于抛物线而言:PF2=x,
∴a1-e1x=e2x-a2=x,
∴消去x得: ?e2-e1=1.
?e2-e1=1.
故选A.
点评:本小题主要考查圆锥曲线的共同特征、圆锥曲线的共同定义的应用、圆锥曲线的几何性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
分析:设椭圆及双曲线的半焦距为c,左右焦点分别为F1、F2,P点的坐标为(x,y).根据圆锥曲线的共同定义,则对于椭圆而言:PF1=a1+e1x,PF2=a1-e1x,对于双曲线而言:PF1=e2x+a2,PF2=e2x-a2,对于抛物线而言:PF2=x,从而建立a1-e1x=e2x-a2=x,消去x化简即得答案.
解答:设椭圆及双曲线的半焦距为c,左右焦点分别为F1、F2,P点的坐标为(x,y).
则对于椭圆而言:PF1=a1+e1x,PF2=a1-e1x,
对于双曲线而言:PF1=e2x+a2,PF2=e2x-a2,
对于抛物线而言:PF2=x,
∴a1-e1x=e2x-a2=x,
∴消去x得:
 ?e2-e1=1.
?e2-e1=1.故选A.
点评:本小题主要考查圆锥曲线的共同特征、圆锥曲线的共同定义的应用、圆锥曲线的几何性质等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
相关题目
 与双曲线
与双曲线 共焦点,点
共焦点,点 在椭圆C上.
在椭圆C上.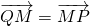 ,求动点M的轨迹方程.
,求动点M的轨迹方程.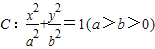 与双曲线
与双曲线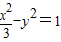 共焦点,点
共焦点,点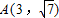 在椭圆C上.
在椭圆C上.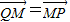 ,求动点M的轨迹方程.
,求动点M的轨迹方程.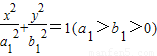 与双曲线
与双曲线 共焦点,点P是该椭圆与双曲线在第一象限的公共点,如果以椭圆的右焦点为焦点,以y轴为准线的抛物线恰过P点,那么椭圆的离心率e1与双曲线的离心率e2之间的关系为( )
共焦点,点P是该椭圆与双曲线在第一象限的公共点,如果以椭圆的右焦点为焦点,以y轴为准线的抛物线恰过P点,那么椭圆的离心率e1与双曲线的离心率e2之间的关系为( )