题目内容
已知函数f(x)=3x,且f(a+2)=18,函数g(x)=3ax-4x的定义域为[0,1].
(1)写出函数g(x)的解析式;
(2)求函数g(x)的单调区间,并用函数单调性的定义给出证明;
(3)求函数g(x)的值域.
答案:
解析:
解析:
解:(1)因为f(x)=3x,所以f(a+2)=3a+2=18,得3a=2.又g(x)=3ax-4x=(3a)x-4x,所以g(x)=2x-4x,x∈[0,1].
(2)令t=2x,y=t-t2=-(t2-t)=-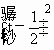 +
+![]() .因为x∈[0,1],且函数t=2x在[0,1]上单调递增,所以t∈[1,2].因为
.因为x∈[0,1],且函数t=2x在[0,1]上单调递增,所以t∈[1,2].因为![]() <1,所以函数y=t-t2在[1,2]上单调递减,所以,函数g(x)的单调递减区间为[0,1].证明如下:任取x1,x2∈[0,1],且x1<x2,则g(x2)-g(x1)=2
<1,所以函数y=t-t2在[1,2]上单调递减,所以,函数g(x)的单调递减区间为[0,1].证明如下:任取x1,x2∈[0,1],且x1<x2,则g(x2)-g(x1)=2![]() -4
-4![]() -2
-2![]() +4
+4![]() =(2
=(2![]() -2
-2![]() )-(2
)-(2![]() -2
-2![]() )(2
)(2![]() +2
+2![]() )=(2
)=(2![]() -2
-2![]() )·(1-2
)·(1-2![]() -2
-2![]() ).因为0≤x1<x2≤1,所以2
).因为0≤x1<x2≤1,所以2![]() >2
>2![]() ,且1≤2
,且1≤2![]() <2,1<2
<2,1<2![]() ≤2,所以2<2
≤2,所以2<2![]() +2
+2![]() <4,所以2
<4,所以2![]() -2
-2![]() >0,且-3<1-2
>0,且-3<1-2![]() -2
-2![]() <-1<0,所以g(x2)-g(x1)<0,即g(x1)>g(x2).故函数g(x)在区间[0,1]上单调递减.
<-1<0,所以g(x2)-g(x1)<0,即g(x1)>g(x2).故函数g(x)在区间[0,1]上单调递减.
(3)因为g(x)在[0,1]上是减函数,所以g(1)≤g(x)≤g(0).因为g(1)=21-41=-2,g(0)=20-40=0,所以-2≤g(x)≤0.所以函数g(x)的值域为[-2,0].

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
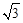 sin ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin ax cos ax+2 cos2 ax的周期为π,其中a>0. sin
ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin
ax cos ax+2 cos2 ax的周期为π,其中a>0. 的最大值;
的最大值; )>kg(x)对x∈[2,4]有解,求实数k的取值范围.
)>kg(x)对x∈[2,4]有解,求实数k的取值范围. sin
ax cos ax+2 cos2 ax的周期为π,其中a>0.
sin
ax cos ax+2 cos2 ax的周期为π,其中a>0. ,无最小值
,无最小值