Question

若曲线y=a|x|与y=x+a(a＞0)有两个公共点，求a的取值范围.

Answer 1

解法一：由

得a|x|=x+a                                                                   ①

（1）若x≥0时，ax=x+a(a-1)x=a.

因为a＞0,x=(a=1时无解)，所以a＞1;

（2）若x＜0,-ax=x+a-(a+1)x=a.

因为a＞0,x=-＜0,可得a＞0或a＜-1(舍去).

由（1）（2）知，当a＞1时，方程组①有两解-和,即方程组有两解，故两曲线有两个公共点，a取值范围为a＞1.

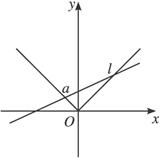
解法二：y=a|x|的曲线是关于y轴对称且顶点在原点的折线C，而y=x+a表示斜率为1且过点（0，a）的直线l.由下图所示可知，当a≤1时，折线C的右支射线与直线l不相交，当a＞1时，l与C的两条射线都相交.所以两曲线有两个相异交点，a的取值范围为a＞1.