题目内容

（极坐标与参数方程选做题）
在极坐标系中，点A的坐标为 $数学公式$ ，曲线C的方程为ρ=2cosθ，则OA（O为极点）所在直线被曲线C所截弦的长度为________．

$\text{[math]}$
分析：先将极坐标化为普通方程求其交点，再据两点间的距离公式求出即可．
解答：由点A的坐标为 $\text{[math]}$ ，∴点A的横坐标x= $\text{[math]}$ =2，纵坐标y= $\text{[math]}$ =2，∴A（2，2），K_0A= $\text{[math]}$ ．
∴直线OA的方程为：y=x．
由曲线C的方程为ρ=2cosθ，则ρ²=2ρcosθ，∴x²+y²=2x．
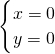联立 $\text{[math]}$ ，解得 $\text{[math]}$ ， $\text{[math]}$ ，∴直线与曲线的交点为（0，0），（1，1）．
因此所求的弦长= $\text{[math]}$ = $\text{[math]}$ ．
故答案为 $\text{[math]}$ ．
点评：本题考查了给出极坐标下直线与圆相交的弦长，掌握转化思想和两点间的距离公式是解决问题的关键．

练习册系列答案

小学课堂作业系列答案

口算练习册系列答案

金博士一点全通系列答案

课时作业本吉林人民出版社系列答案

天天向上中考零距离教材新解系列答案

阳光互动绿色成长空间系列答案

星火英语Spark巅峰训练系列答案

名师点津随堂小测系列答案

好帮手阅读成长系列答案

超越训练系列答案

相关题目

（极坐标与参数方程选做题）极坐标方程为ρ=2cosθ的圆与参数方程为

的直线位置关系是

A．（不等式选讲选做题）函数y=|x+1|+|x-1|的最小值是

B．（几何证明选讲选做题）如图，PA切圆O于点A，割线PBC经过圆心O，OB=PB=1，OA绕点O逆时针转60°到OD，则PD的长为

．
C．（极坐标与参数方程选做题）在极坐标系中，过圆ρ=6cosθ的圆心，且垂直于极轴的直线的极坐标方程为

（2012•月湖区模拟）①（极坐标与参数方程选讲选做题）已知点P（1+cosα，sinα），参数α∈[0，π]，点Q在曲线C：ρ=

上，则点P与点Q之间距离的最小值为

．
②（不等式选讲选做题）若存在实数x满足|x-3|+|x-m|＜5，则实数m的取值范围是

选修4-4：极坐标与参数方程选讲
已知：曲线C的极坐标方程为：ρ=acosθ（a＞0），直线?的参数方程为：

（t为参数）
（1）求曲线C与直线?的普通方程；
（2）若直线?与曲线C相切，求a值．

（极坐标与参数方程选做题）
已知曲线C₁的极坐标方程为ρ=6cosθ，曲线C₂的极坐标方程为θ=

（ρ∈R，曲线C₁、C₂相交于点A，B，则弦AB的长为