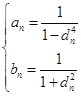题目内容
【题目】已知椭圆
过点
离心率为
.
（1）求
的方程；
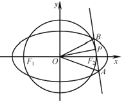
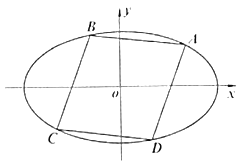
（2）如图，若菱形
内接于椭圆，求菱形面积的最小值.
【答案】（1）
；（2）4
【解析】
（1）把点的坐标代入椭圆方程中，再根据离心率，建立方程组，求解方程组即可；
（2）当
与
轴或
轴重合时，利用菱形面积计算求解即可；
当直线存在斜率且不为零时，设出直线方程，与椭圆方程联立，求出弦长，最后利用菱形的面积公式求出表达式，结合基本不等式进行求解即可，最后求出菱形面积最小值.
解：（1）由题意得
又
解得
，
.
所以
的方程为
（2）①当与轴或轴重合时，可求菱形
的面积为
；
②当为
时，
为
，由
得
，
所以由弦长公式得
，
同理可得
所以菱形的面积为
∵
∴
，当且仅当
时取等号.
∵
∴菱形面积的最小值为4. （说明：本题也可三角换元法或求导法求最小值）
练习册系列答案
相关题目
