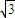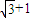题目内容
点P为双曲线C1：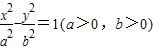
和圆C2：x2+y2=a2+b2的一个交点，且2∠PF1F2=∠PF2F1，其中F1，F2为双曲线C1的两个焦点，则双曲线C1的离心率为（ ）A．
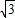
B．
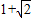
C．
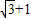
D．2
【答案】分析：由题意：PF1⊥PF2，且2∠PF1F2=∠PF2F1，故∠PF1F2=30°，∠PF2F1=60°．设|PF2|=m，则|PF1|=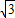
m，|F1F2|=2m．由e=
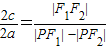，能求出双曲线的离心率．
解答：解：由题意：PF1⊥PF2，且2∠PF1F2=∠PF2F1，
∴∠PF1F2=30°，∠PF2F1=60°．
设|PF2|=m，
则|PF1|=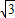
m，
|F1F2|=2m．
e=
=
=
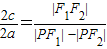
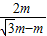
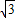+1．
故选C．
点评：本题考查双曲线的离心率的求法，解题时要认真审题，灵活运用双曲线的性质，合理地进行等价转化．
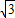m，|F1F2|=2m．由e=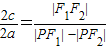，能求出双曲线的离心率．解答：解：由题意：PF1⊥PF2，且2∠PF1F2=∠PF2F1，
∴∠PF1F2=30°，∠PF2F1=60°．
设|PF2|=m，
则|PF1|=
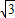m，|F1F2|=2m．
e=
=
=
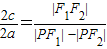
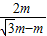
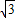+1．故选C．
点评：本题考查双曲线的离心率的求法，解题时要认真审题，灵活运用双曲线的性质，合理地进行等价转化．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
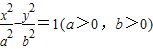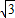
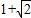
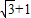
和圆C2：x2+y2=a2+b2的一个交点，且2∠PF1F2=∠PF2F1，其中F1，F2为双曲线C1的两个焦点，则双曲线C1的离心率为（ ）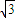
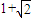
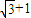
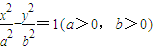和圆C2：x2+y2=a2+b2的一个交点，且2∠PF1F2=∠PF2F1，其中F1，F2为双曲线C1的两个焦点，则双曲线C1的离心率为（ ）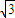
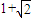
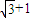
和圆C2：x2+y2=a2+b2的一个交点，且2∠PF1F2=∠PF2F1，其中F1，F2为双曲线C1的两个焦点，则双曲线C1的离心率为（ ）
和圆C2：x2+y2=a2+b2的一个交点，且2∠PF1F2=∠PF2F1，其中F1，F2为双曲线C1的两个焦点，则双曲线C1的离心率为（ ）
