题目内容
函数 在区间[
在区间[ ]的最小值为 .
]的最小值为 .
【答案】分析:遇到三角函数性质问题,首先要把所给的函数式变换为y=Asin(ωx+φ)的形式,本题变化时用到两角和的正弦公式,当自变量取值为【0, 】时,做出括号内的变量的取值,得出结果.
】时,做出括号内的变量的取值,得出结果.
解答:解:y=sinx+ cosx
cosx
=2( sinx+
sinx+ cosx)
cosx)
=2sin(x+ ),
),
∵ ,
,
∴ ,
,
∴ ,
,
∴最小值为1,
故答案为:1.
点评:给定自变量的取值,要我们计算三角函数值,这是对性质的考查,解题时注意把所给的函数式同三角函数对应起来.
 】时,做出括号内的变量的取值,得出结果.
】时,做出括号内的变量的取值,得出结果.解答:解:y=sinx+
 cosx
cosx=2(
 sinx+
sinx+ cosx)
cosx)=2sin(x+
 ),
),∵
 ,
,∴
 ,
,∴
 ,
,∴最小值为1,
故答案为:1.
点评:给定自变量的取值,要我们计算三角函数值,这是对性质的考查,解题时注意把所给的函数式同三角函数对应起来.

练习册系列答案
相关题目
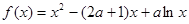
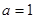 时, 求函数
时, 求函数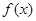 的单调增区间;
的单调增区间;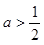 时,求函数
时,求函数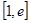 上的最小值;
上的最小值;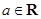 ,函数
,函数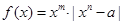 .
.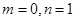 ,写出函数
,写出函数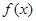 的单调递增区间(不必证明);
的单调递增区间(不必证明); ,当
,当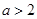 时,求函数
时,求函数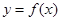 在区间
在区间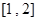 上的最小值.
上的最小值.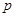 :函数
:函数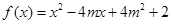 在区间
在区间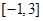 上的最小值等于2;命题
上的最小值等于2;命题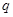 :不等式
:不等式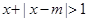 对于任意
对于任意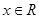 恒成立,如果上述两命题中有且仅有一个真命题,试求实数
恒成立,如果上述两命题中有且仅有一个真命题,试求实数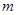 的取值范围。
的取值范围。