题目内容
若函数y=x2+（a+1）x-1在[-2，2]上单调，则a的范围是（ ）
| A．a≥3 | B．a≤-5 | C．a≥3或a≤-5 | D．a＞3或a＜-5 |
∵函数y=x2+（a+1）x-1的对称轴为 x=-
，且函数在区间[-2，2]上是单调函数，
∴-
≤-2或-
≥2，解得 a≥3或a≤-5，
故实数a的取值范围是 （-∞，-5]∪[3，+∞），
故答案为 C
| a+1 |
| 2 |
∴-
| a+1 |
| 2 |
| a+1 |
| 2 |
故实数a的取值范围是 （-∞，-5]∪[3，+∞），
故答案为 C
练习册系列答案
优等生题库系列答案
53天天练系列答案
相关题目
，则下列不等式成立的是（ ）
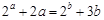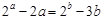，则
，则