题目内容
已知函数 .
.
见解析
解析试题分析:证明:设 ,
,
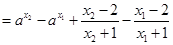
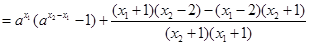
 .
.
因为 ,又
,又 ,所以
,所以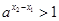 .
.
而 ,所以
,所以 ,
, ,
,
所以 ,
,
即得 在
在 上为增函数.
上为增函数.
考点:本题主要考查演绎推理的意义及方法,定义法证明函数单调性。
点评:明确推理格式,力求层次分明。

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
题目内容
已知函数 .
.
见解析
解析试题分析:证明:设 ,
,
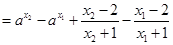
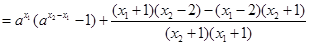
 .
.
因为 ,又
,又 ,所以
,所以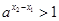 .
.
而 ,所以
,所以 ,
, ,
,
所以 ,
,
即得 在
在 上为增函数.
上为增函数.
考点:本题主要考查演绎推理的意义及方法,定义法证明函数单调性。
点评:明确推理格式,力求层次分明。

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案