题目内容
如图, 平面 平面
平面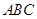 ,
, 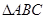 是以
是以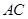 为斜边的等腰直角三角形,
为斜边的等腰直角三角形, 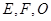 分别为
分别为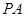 ,
, 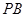 ,
, 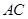 的中点,
的中点, 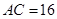 ,
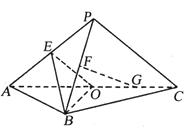
, 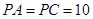 .
.
(1) 设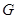 是
是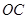 的中点, 证明:
的中点, 证明: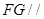 平面
平面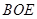 ;
;
(2) 证明:在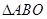 内存在一点
内存在一点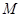 , 使
, 使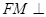 平面
平面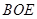 , 并求点
, 并求点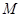 到
到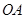 ,
, 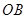 的距离.
的距离.
(1)建立直角坐标系,利用向量的数量积为零来得到证明。
(2)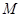 到
到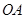 ,
, 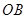 的距离为
的距离为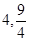 .
.
解析试题分析:证明:
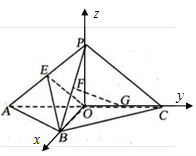
(I) 如图, 连结OP, 以O为坐标原点, 分别以OB、OC、OP所在直线为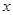 轴,
轴, 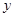 轴,
轴, 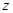 轴, 建立空间直角
轴, 建立空间直角
坐标系O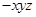 ,
, 
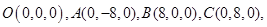
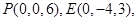
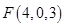 , -2分
, -2分
由题意得, 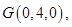 因
因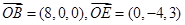 ,
,
因此平面BOE的法向量为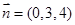 , 4分
, 4分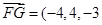 得
得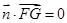 , 又直线
, 又直线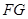 不在平面
不在平面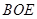 内,
内,
因此有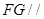 平面
平面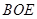 6分
6分
(II)设点M的坐标为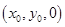 , 则
, 则 , 因为
, 因为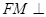 平面BOE, 所以有
平面BOE, 所以有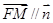 , 因此有
, 因此有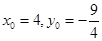 , 即点M的坐标为
, 即点M的坐标为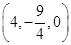 , 9分
, 9分
在平面直角坐标系 中,
中, 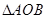 的内部区域满足不等式组
的内部区域满足不等式组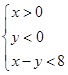 , 经检验, 点M的坐标满足上述不等式组, 所以在
, 经检验, 点M的坐标满足上述不等式组, 所以在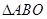 内存在一点
内存在一点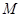 , 使
, 使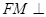 平面
平面 , 11分
, 11分
由点M的坐标得点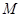 到
到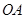 ,
, 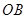 的距离为
的距离为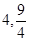 . 12分
. 12分
考点:距离和垂直的证明
点评:主要是考查了空间直角坐标系中直线的垂直,以及点到直线距离的求解,属于中档题。

练习册系列答案
相关题目
 中,
中, ⊥底面
⊥底面 ,四边形
,四边形 ⊥
⊥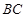 ,
, ,
,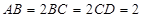 .
.
 ⊥平面
⊥平面 ;
;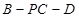 的余弦值为
的余弦值为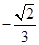 ,求
,求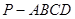 ,底面
,底面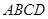 是边长为
是边长为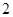 的正方形,
的正方形,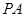 ⊥面
⊥面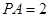 ,过点
,过点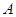 作
作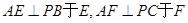 ,连接
,连接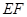 .
. ;
;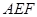 交侧棱
交侧棱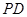 于点
于点 ,求多面体
,求多面体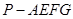 的体积.
的体积.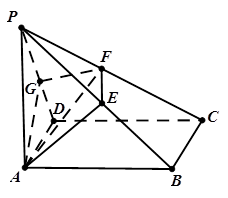
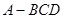 ,平面
,平面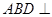 平面
平面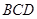 ,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC
,AB=AD=1,AB⊥AD,DB=DC,DB⊥DC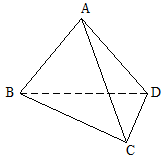
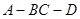 的正切值.
的正切值.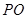 中,已知
中,已知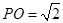 ,⊙O的直径
,⊙O的直径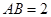 ,
,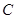 是
是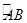 的中点,
的中点,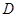 为
为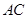 的中点.
的中点.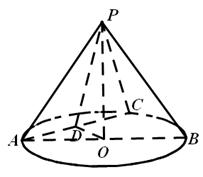
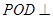 平面
平面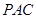 ;
; 的余弦值.
的余弦值. 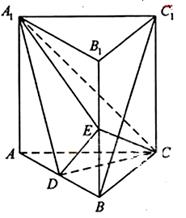
 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积. 的侧面积为
的侧面积为 ,若
,若 .
.
 与平面
与平面 所成角的大小.
所成角的大小. 的底面
的底面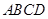 是边长为2的菱形,
是边长为2的菱形,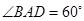 .已知
.已知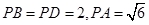 .
.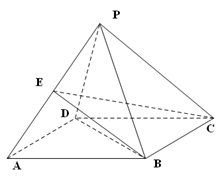
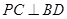
 为
为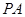 的中点,求三菱锥
的中点,求三菱锥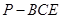 的体积.
的体积.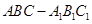 中,
中,

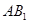 与
与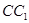 所成角的大小;
所成角的大小;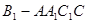 的体积。
的体积。