题目内容
已知向量 ,
, 满足|
满足| |=2|
|=2| |≠0,且关于x的函数f(x)=2x3+3|
|≠0,且关于x的函数f(x)=2x3+3| |x2+6
|x2+6 •
• x+5 在实数集R上单调递增,则向量
x+5 在实数集R上单调递增,则向量 ,
, 的夹角的取值范围是
的夹角的取值范围是
- A.[0.
 ]
] - B.[0,
 ]
] - C.(0,
 ]
] - D.[
 ,π]
,π]
B
分析:求导数,利用函数f(x)=2x3+3|a|x2+6a•bx+5 在实数集R上单调递增,可得判别式小于等于0在R上恒成立,再利用| |=2|
|=2| |≠0,利用向量的数量积,即可得到结论.
|≠0,利用向量的数量积,即可得到结论.
解答:求导数可得f′(x)=6x2+6| |x+6
|x+6  ,则由函数f(x)=2x3+3|a|x2+6a•bx+5 在实数集R上单调递增,
,则由函数f(x)=2x3+3|a|x2+6a•bx+5 在实数集R上单调递增,
可得f′(x)=6x2+6| |x+6
|x+6  ≥0恒成立,即 x2+|
≥0恒成立,即 x2+| |x+
|x+ ≥0恒成立,故判别式△=
≥0恒成立,故判别式△= -4
-4 ≤0 恒成立,
≤0 恒成立,
再由| |=2|
|=2| |≠0,可得 4
|≠0,可得 4  ≤8|
≤8| |•|
|•| |cos<
|cos< ,
, >,
>,
∴cos< ,
, >≥
>≥ ,
,
∴< ,
, >∈[0,
>∈[0, ],
],
故选B.
点评:本题考查导数知识的运用,考查函数的单调性,考查向量的数量积,解题的关键是利用判别式小于等于0在R上恒成立,属于中档题.
分析:求导数,利用函数f(x)=2x3+3|a|x2+6a•bx+5 在实数集R上单调递增,可得判别式小于等于0在R上恒成立,再利用|
 |=2|
|=2| |≠0,利用向量的数量积,即可得到结论.
|≠0,利用向量的数量积,即可得到结论.解答:求导数可得f′(x)=6x2+6|
 |x+6
|x+6  ,则由函数f(x)=2x3+3|a|x2+6a•bx+5 在实数集R上单调递增,
,则由函数f(x)=2x3+3|a|x2+6a•bx+5 在实数集R上单调递增,可得f′(x)=6x2+6|
 |x+6
|x+6  ≥0恒成立,即 x2+|
≥0恒成立,即 x2+| |x+
|x+ ≥0恒成立,故判别式△=
≥0恒成立,故判别式△= -4
-4 ≤0 恒成立,
≤0 恒成立,再由|
 |=2|
|=2| |≠0,可得 4
|≠0,可得 4  ≤8|
≤8| |•|
|•| |cos<
|cos< ,
, >,
>,∴cos<
 ,
, >≥
>≥ ,
,∴<
 ,
, >∈[0,
>∈[0, ],
],故选B.
点评:本题考查导数知识的运用,考查函数的单调性,考查向量的数量积,解题的关键是利用判别式小于等于0在R上恒成立,属于中档题.

练习册系列答案
相关题目
 、
、 满足
满足 ,则
,则 .
. ,实数
,实数 满足
满足 ,则
,则 的最小值为( )
的最小值为( ) B.1 C.
B.1 C. D.
D.
 ,
, 满足
满足 ,
, ,
, ,则
,则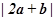 的值为_______.
的值为_______.