Question

已知函数f（x）=

1 2 x+ 1 2   (x≤1)  x2-6x+5    (x＞1)

，集合A={x|f（x）＞0}，集合B={x|log

1

2

（x-a）＞1}．
（Ⅰ）画出函数f（x）的图象，并根据图象写出不等式f（x）＞0的解集；
（Ⅱ）若B⊆A，求实数a的取值范围．

Answer 1

分析：（Ⅰ）根据一次函数、二次函数图象，分段画出后，即可得出f（x）的图象
（Ⅱ）根据集合的基本关系，转化为集合中元素的关系，得出相关的不等式（组），并求解即可．

解答：解：（Ⅰ）如图

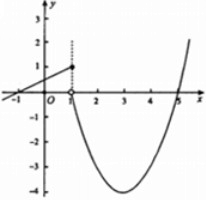
根据图象得不等式f（x）＞0的解集为（-1，1]∪（5，+∞）
（Ⅱ）由（Ⅰ）得集合A=（-1，1]∪（5，+∞）
由log

1

2

（x-a）＞1，

1

2

＞x-a＞0，a+

1

2

＞x＞a，
集合B=（a，a+

1

2

）
∵B⊆A，∴

a≥-1 a+ 1 2 ≤1

或a≥5
解得-1≤a≤

1

2

或a≥5．
实数a的取值范围为-1≤a≤

1

2

或a≥5．

点评：本题考查函数的图象，集合的基本关系，数形结合的思想．考查转化、计算、逻辑思维能力．