Question

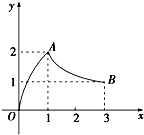
函数f（x）的图象是如图所示的折线段OAB，点A坐标为（1，2），点B坐标为（3，0）．定义函数g（x）=f（x）•（x-1）．则函数g（x）最大值为

1. A.
   0
2. B.
   2
3. C.
   1
4. D.
   4

Answer 1

C
分析：本题考查的是分段函数问题．在解答的过程当中应先根据函数f（x）的图象求出解析式，再根据g（x）=f（x）•（x-1）．求的函数g（x）的解析式，结合函数g（x）的解析式即可求的函数g（x）最大值．
解答：由题意知：函数f（x）的解析式为：，
又∵g（x）=f（x）•（x-1）．
∴函数g（x）的解析式为：

当0≤x≤1时，，∴g_max（x）=g（1）=g（0）=0；
当1＜x≤3时，g（x）=-（x-2）²+1＜1．
∴函数g（x）最大值为1．
故选C．
点评：本题考查的是分段函数解析式的求法和分段函数求最值的综合问题．在解答时充分体现了数形结合的思想、新定义的思想、分类讨论的思想以及问题转化的思想．值得同学们体会反思．