题目内容
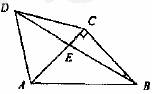
如图△ACD是等边三角形，△ABC是等腰直角三角形，∠ACB=90°，BD交AC于E，AB=2
（Ⅰ）求cos∠CBE的值；
（Ⅱ）求AE。
解：（Ⅰ）因为∠BCD=90º+60º=150º，CB=AC=CD，
所以∠CBE=15º，
所以cos∠CBE=cos（45º－30º）=
（Ⅱ）在△ABE中，AB=2，
由正弦定理
，
故
.
练习册系列答案
相关题目
题目内容
如图△ACD是等边三角形，△ABC是等腰直角三角形，∠ACB=90°，BD交AC于E，AB=2
（Ⅰ）求cos∠CBE的值；
（Ⅱ）求AE。
解：（Ⅰ）因为∠BCD=90º+60º=150º，CB=AC=CD，
所以∠CBE=15º，
所以cos∠CBE=cos（45º－30º）=
（Ⅱ）在△ABE中，AB=2，
由正弦定理，
故.
如图（1），C是直径AB=2的⊙O上一点，AD为⊙O的切线，A为切点，△ACD为等边三角形，连接DO交AC于E，以AC为折痕将△ACD翻折到图（2）的△ACP位置，点P为平面ABC外的点．
如图（1），C是直径AB=2的⊙O上一点，AD为⊙O的切线，A为切点，△ACD为等边三角形，连接DO交AC于E，以AC为折痕将△ACD翻折到图（2）的△ACP位置．
，求三棱锥P-AOF的体积．
，求二面角A-PC-B的正弦值．
，求三棱锥P-AOF的体积．