题目内容
设p为常数,函数f(x)=log2(1-x)+plog2(1+x)为奇函数.
(1)求p的值;(2)若f(x)>2,求x的取值范围;(3)求证:x•f(x)≤0.
(1)求p的值;(2)若f(x)>2,求x的取值范围;(3)求证:x•f(x)≤0.
(1)f(x)=log2(1-x)+plog2(1+x)=log2[(1-x)(1+x)p],
∵f(x)=log2(1-x)+plog2(1+x)为奇函数,
∴f(-x)=log2[(1+x)(1-x)p]=-f(x)=log2
=log2[(1-x)-1(1+x)-p],
∴
,
∴p=-1.
(2)∵p=-1,
∴f(x)=log2
,
∵f(x)>2,
∴
,
解得-1<x<-
,
∴f(x)>2时x的取值范围是(-1,-
).
(3)∵f(x)=log2
,
∴
>0,解得-1<x<1.
当-1<x<0时,
>1,f(x)=log2
>0,
∴x•f(x)<0;
当x=0时,
=1,f(x)=log2
=0,
∴x•f(x)=0;
当0<x<1时,
<1,f(x)=log2
<0,
∴x•f(x)<0.
综上所述,x•f(x)≤0.
∵f(x)=log2(1-x)+plog2(1+x)为奇函数,
∴f(-x)=log2[(1+x)(1-x)p]=-f(x)=log2
| 1 |
| (1-x)(1+x )p |
∴
|
∴p=-1.
(2)∵p=-1,
∴f(x)=log2
| 1-x |
| 1+x |
∵f(x)>2,
∴
|
解得-1<x<-
| 3 |
| 5 |
∴f(x)>2时x的取值范围是(-1,-
| 3 |
| 5 |
(3)∵f(x)=log2
| 1-x |
| 1+x |
∴
| 1-x |
| 1+x |
当-1<x<0时,
| 1-x |
| 1+x |
| 1-x |
| 1+x |
∴x•f(x)<0;
当x=0时,
| 1-x |
| 1+x |
| 1-x |
| 1+x |
∴x•f(x)=0;
当0<x<1时,
| 1-x |
| 1+x |
| 1-x |
| 1+x |
∴x•f(x)<0.
综上所述,x•f(x)≤0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
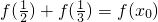 ,求x0的值;
,求x0的值; ,求x的值;
,求x的值;