题目内容
已知中心在原点,一焦点为F(0,
解:∵椭圆的中心在原点,焦点在y轴上,
∴椭圆的方程为标准方程.
∵c=![]() ,∴a2=b2+50.
,∴a2=b2+50.
∴椭圆的方程可写成![]() +
+![]() =1.
=1.
把直线y=3x-2代入椭圆的方程并整理得
10(b2+5)x2-12b2x-b4-46b2=0.
∴x1+x2=![]() .
.
∵弦的中点的横坐标为![]() ,
,
∴![]() =1,b2=25.
=1,b2=25.
∴a2=75.
∴所求椭圆的方程为![]() =1.
=1.
点评:解决直线被圆锥曲线截得的弦的中点问题,经常用到韦达定理.

练习册系列答案
相关题目
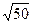 )的椭圆被直线
)的椭圆被直线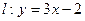 截得的弦的中点横坐标为
截得的弦的中点横坐标为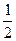 ,求此椭圆的方程。
,求此椭圆的方程。 有共同的渐近线,且过点
有共同的渐近线,且过点 的双曲线的方程。
的双曲线的方程。 )的椭圆被直线L:y=3x-2截得的弦的中点的横坐标为
)的椭圆被直线L:y=3x-2截得的弦的中点的横坐标为 ,求此椭圆的方程。
,求此椭圆的方程。 )的椭圆被直线
)的椭圆被直线 截得的弦的中点横坐标为
截得的弦的中点横坐标为 ,求此椭圆的方程。
,求此椭圆的方程。 )的椭圆被直线l:y=3x-2截得的弦的中点横坐标为
)的椭圆被直线l:y=3x-2截得的弦的中点横坐标为 ,求此椭圆的方程。
,求此椭圆的方程。