题目内容
(本小题满分12分)已知椭圆C的中心为坐标原点O,焦点在y轴上,离心率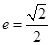 ,椭圆上的点到焦点的最短距离为
,椭圆上的点到焦点的最短距离为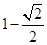 , 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且
, 直线l与y轴交于点P(0,m),与椭圆C交于相异两点A、B,且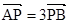 .
.
(1)求椭圆方程;
(2)求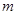 的取值范围.
的取值范围.
【答案】
解:(1)设C: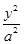 +
+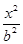 =1(a>b>0),设c>0,c2=a2-b2,由条件知a-c=
=1(a>b>0),设c>0,c2=a2-b2,由条件知a-c= ,
, =
= ,………1分
,………1分
∴a=1,b=c= ………………………………………3分
………………………………………3分
故C的方程为:y2+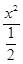 =1
……………………………4分
=1
……………………………4分
(2)当直线斜率不存在时: ……………………………………5分
……………………………………5分
当直线斜率存在时:设l与椭圆C交点为A(x1,y1),B(x2,y2)
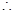
 得(k2+2)x2+2kmx+(m2-1)=0 …………………6分
得(k2+2)x2+2kmx+(m2-1)=0 …………………6分
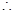 Δ=(2km)2-4(k2+2)(m2-1)=4(k2-2m2+2)>0
(*)………………7分
Δ=(2km)2-4(k2+2)(m2-1)=4(k2-2m2+2)>0
(*)………………7分
x1+x2= , x1x2=
, x1x2= …………………………………8分
…………………………………8分
∵ =3
=3 ∴-x1=3x2 ∴
∴-x1=3x2 ∴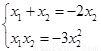
消去x2,得3(x1+x2)2+4x1x2=0,∴3( )2+4
)2+4 =0……………………9分
=0……………………9分
整理得4k2m2+2m2-k2-2=0
m2=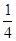 时,上式不成立;m2≠
时,上式不成立;m2≠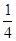 时,k2=
时,k2= , …………………10分
, …………………10分
∴k2=
 0,∴
0,∴ 或
或
高三数学(理工类)参考答案第3页(共4页)
把k2= 代入(*)得
代入(*)得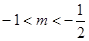 或
或
∴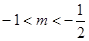 或
或 ……………………………………11分
……………………………………11分
综上m的取值范围为 或
或 ……………………………12分
……………………………12分
【解析】略

练习册系列答案
相关题目