题目内容
已知f(x)=ax3+3x2-x+1在R上是减函数,求a的取值范围。
解:函数f(x)的导数: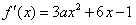 ,
,
(Ⅰ)当f′(x)<0(x∈R)时,f(x)是减函数,
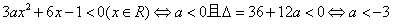 ,
,
所以,当a<-3时,由f′(x)<0,知f(x)(x∈R)是减函数;
(Ⅱ)当a=-3时,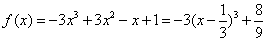 ,
,
由函数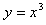 在R上的单调性,
在R上的单调性,
可知当a=-3时,f(x)(x∈R)是减函数;
(Ⅲ)当a>-3时,在R上存在一个区间,其上有f′(x)>0,
所以,当a>-3时,函数f(x)(x∈R)不是减函数;
综上,所求a的取值范围是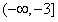 。
。
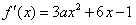 ,
,(Ⅰ)当f′(x)<0(x∈R)时,f(x)是减函数,
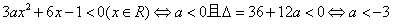 ,
,所以,当a<-3时,由f′(x)<0,知f(x)(x∈R)是减函数;
(Ⅱ)当a=-3时,
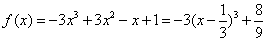 ,
,由函数
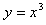 在R上的单调性,
在R上的单调性,可知当a=-3时,f(x)(x∈R)是减函数;
(Ⅲ)当a>-3时,在R上存在一个区间,其上有f′(x)>0,
所以,当a>-3时,函数f(x)(x∈R)不是减函数;
综上,所求a的取值范围是
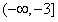 。
。
练习册系列答案
相关题目
已知F(x)=ax3+bx5+cx3+dx-6,F(-2)=10,则F(2)的值为( )
| A、-22 | B、10 | C、-10 | D、22 |