题目内容
 如图,要建一间体积为75m3,墙高为3m的长方体形的简易仓库.已知仓库屋顶每平方米的造价为500元,墙壁每平方米的造价为400元,地面造价忽略不计.问怎样设计仓库地面的长与宽,能使总造价最低?最低造价是多少?
如图,要建一间体积为75m3,墙高为3m的长方体形的简易仓库.已知仓库屋顶每平方米的造价为500元,墙壁每平方米的造价为400元,地面造价忽略不计.问怎样设计仓库地面的长与宽,能使总造价最低?最低造价是多少?分析:先确定仓库屋顶的面积、墙壁的面积,可得仓库的总造价,利用基本不等式,即可求最值.
解答:解:设仓库地面的长为x(x>0)m,宽为y(y>0)m,则有3xy=75,所以y=
. …(2分)
则仓库屋顶的面积为xy m2,墙壁的面积为6(x+y) m2.
所以仓库的总造价W=500xy+400×6(x+y),…(5分)
将y=
代入上式,整理得W=12500+2400(x+
). …(7分)
因为x>0,
所以W=12500+2400(x+
)≥12500+2400×2
=36500,…(10分)
且当x=
,即x=5时,W取得最小值36500.
此时y=
=5. …(12分)
答:当仓库地面的长为5m,宽为5m时,仓库的总造价最低,最低造价为36500元.…(13分)
| 25 |
| x |
则仓库屋顶的面积为xy m2,墙壁的面积为6(x+y) m2.
所以仓库的总造价W=500xy+400×6(x+y),…(5分)
将y=
| 25 |
| x |
| 25 |
| x |
因为x>0,
所以W=12500+2400(x+
| 25 |
| x |
x×
|
且当x=
| 25 |
| x |
此时y=
| 25 |
| x |
答:当仓库地面的长为5m,宽为5m时,仓库的总造价最低,最低造价为36500元.…(13分)
点评:本题考查利用数学知识解决实际问题,考查基本不等式的运用,确定函数模型是关键.

练习册系列答案
相关题目
 ,墙高为
,墙高为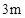 的长方体形的简易仓库. 已知仓库屋顶每平方米的造价为500元,墙壁每平方米的造价为400元,地面造价忽略不计. 问怎样设计仓库地面的长与宽,能使总造价最低?最低造价是多少?
的长方体形的简易仓库. 已知仓库屋顶每平方米的造价为500元,墙壁每平方米的造价为400元,地面造价忽略不计. 问怎样设计仓库地面的长与宽,能使总造价最低?最低造价是多少?
 如图,要建一间体积为75m3,墙高为3m的长方体形的简易仓库.已知仓库屋顶每平方米的造价为500元,墙壁每平方米的造价为400元,地面造价忽略不计.问怎样设计仓库地面的长与宽,能使总造价最低?最低造价是多少?
如图,要建一间体积为75m3,墙高为3m的长方体形的简易仓库.已知仓库屋顶每平方米的造价为500元,墙壁每平方米的造价为400元,地面造价忽略不计.问怎样设计仓库地面的长与宽,能使总造价最低?最低造价是多少?