题目内容
已知函数f(x)=ex-x(e为自然对数的 底数)。
(1)求f(x)的最小值;
(2)不等式f(x)>ax的解集为P,若M={x|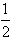 ≤x≤2}且M∩P≠
≤x≤2}且M∩P≠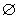 ,求实数a的取值范围;
,求实数a的取值范围;
(3)已知n∈N*,且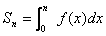 ,是否存在等差数列{an} 和首项为f(1),公比大于0的等比数列{bn},使得a1+a2+…+an+b1+b2+…+bn=Sn?若存在,请求出数列{an}、{bn}的通项公式;若不存在,请说明理由。
,是否存在等差数列{an} 和首项为f(1),公比大于0的等比数列{bn},使得a1+a2+…+an+b1+b2+…+bn=Sn?若存在,请求出数列{an}、{bn}的通项公式;若不存在,请说明理由。
(1)求f(x)的最小值;
(2)不等式f(x)>ax的解集为P,若M={x|
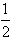 ≤x≤2}且M∩P≠
≤x≤2}且M∩P≠ ,求实数a的取值范围;
,求实数a的取值范围;(3)已知n∈N*,且
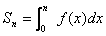 ,是否存在等差数列{an} 和首项为f(1),公比大于0的等比数列{bn},使得a1+a2+…+an+b1+b2+…+bn=Sn?若存在,请求出数列{an}、{bn}的通项公式;若不存在,请说明理由。
,是否存在等差数列{an} 和首项为f(1),公比大于0的等比数列{bn},使得a1+a2+…+an+b1+b2+…+bn=Sn?若存在,请求出数列{an}、{bn}的通项公式;若不存在,请说明理由。解:(1)f'(x)=ex-1
由f'(x)=0,得x=0
当x>0时,f'(x)>0;
当x<0时,f'(x)<0
∴f(x)在(0,+∞)上递增,在(-∞,0)上递减
∴f(x)min=f(0)=1。
(2)∵M∩P≠ ,
,
∴f(x)>ax在区间 上有解,
上有解,
由f(x)>ax,得ex-x>ax即 在
在 上有解
上有解
令
则
∴g(x)在 上递减,在[1,2]上递增
上递减,在[1,2]上递增
又
且
∴
∴ 。
。
(3)假设存在公差为d的等差数列{an}和公比q>0,首项为f(1)的等比数列{bn},使a1+a2+…+an+b1+b2+…+ bn=Sn
∵
b1=f(1)=e-1,
∴a1+b1=S1即
∴
又n≥2时

故n=2,3时有

②-①×2得q2-2q=e2-2e,解得q=e或q=2-e(舍),
故q=e,d=-1,
此时

且

∴存在这样的数列{an}、{bn}满足题意。
由f'(x)=0,得x=0
当x>0时,f'(x)>0;
当x<0时,f'(x)<0
∴f(x)在(0,+∞)上递增,在(-∞,0)上递减
∴f(x)min=f(0)=1。
(2)∵M∩P≠
 ,
,∴f(x)>ax在区间
 上有解,
上有解,由f(x)>ax,得ex-x>ax即
 在
在 上有解
上有解令

则

∴g(x)在
 上递减,在[1,2]上递增
上递减,在[1,2]上递增又

且

∴

∴
 。
。(3)假设存在公差为d的等差数列{an}和公比q>0,首项为f(1)的等比数列{bn},使a1+a2+…+an+b1+b2+…+ bn=Sn
∵

b1=f(1)=e-1,
∴a1+b1=S1即

∴

又n≥2时

故n=2,3时有

②-①×2得q2-2q=e2-2e,解得q=e或q=2-e(舍),
故q=e,d=-1,
此时


且


∴存在这样的数列{an}、{bn}满足题意。

练习册系列答案
相关题目