题目内容
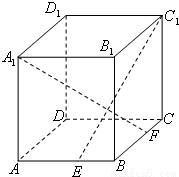
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 .①AC∥平面CB1D1;
②AC1⊥平面CB1D1;
③AC1与底面ABCD所成角的正切值是
 ;
;④AD1与BD为异面直线.

【答案】分析:由AC∩平面CB1D1=C,能判断①不正确;由正方体的性质和直线与平面垂直的判定定理,能判断②正确;由线面角的求法能判断③正确;由异面直线判定定理,能判断④正确.
解答:解:由ABCD-A1B1C1D1为正方体,知:
①∵AC∩平面CB1D1=C,∴AC与平面CB1D1相交,故①不正确;
②由正方体的性质,得B1D1⊥A1C1,CC1⊥B1D1,故B1D1⊥平面 ACC1A1,故 B1D1⊥AC1.
同理可得 B1C⊥AC1.再根据直线和平面垂直的判定定理可得,AC1⊥平面CB1D1 ,故②正确;
③AC1与底面ABCD所成角的正切值tan =
= ,故③正确;
,故③正确;
④∵AD1∩平面ABCD=A,BD?平面ABCD,A∉BD,
∴由异面直线判定理,知AD1与BD为异面直线,故④正确.
故答案为:②③④.
点评:本题考查直线与直线、直线与平面的位置关系的判断,解题时要认真审题,注意异面直线的判定,直线和平面平行、垂直的判定定理的应用.
解答:解:由ABCD-A1B1C1D1为正方体,知:
①∵AC∩平面CB1D1=C,∴AC与平面CB1D1相交,故①不正确;
②由正方体的性质,得B1D1⊥A1C1,CC1⊥B1D1,故B1D1⊥平面 ACC1A1,故 B1D1⊥AC1.
同理可得 B1C⊥AC1.再根据直线和平面垂直的判定定理可得,AC1⊥平面CB1D1 ,故②正确;
③AC1与底面ABCD所成角的正切值tan
 =
= ,故③正确;
,故③正确;④∵AD1∩平面ABCD=A,BD?平面ABCD,A∉BD,
∴由异面直线判定理,知AD1与BD为异面直线,故④正确.
故答案为:②③④.
点评:本题考查直线与直线、直线与平面的位置关系的判断,解题时要认真审题,注意异面直线的判定,直线和平面平行、垂直的判定定理的应用.

练习册系列答案
相关题目
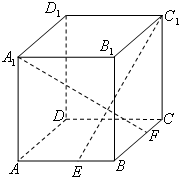 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是