题目内容
（2012•孝感模拟）已知命题p：?x∈R，使sinx=
；命题q：?x∈R，都有x2+x+1＞0．下列结论：
①命题“p∧q”是真命题
②命题“￢p∨q”是真命题
③命题“￢p∨￢q”是假命题
④命题“p∧￢q”是假命题
其中正确的是（ ）
| ||
| 2 |
①命题“p∧q”是真命题
②命题“￢p∨q”是真命题
③命题“￢p∨￢q”是假命题
④命题“p∧￢q”是假命题
其中正确的是（ ）
分析：根据正弦函数的性质可知命题p：?x∈R，使sinx=
为假命题，￢p为真命题；
由于x2+x+1=(x+
)2+
＞0恒成立，则可得命题q：?x∈R，都有x2+x+1＞0为真命题，￢q为假命题
根据复合命题的真假关系即可判断
| ||
| 2 |
由于x2+x+1=(x+
| 1 |
| 2 |
| 3 |
| 4 |
根据复合命题的真假关系即可判断
解答：解：命题p：?x∈R，使sinx=
为假命题，￢p为真命题；
由于x2+x+1=(x+
)2+
＞0恒成立，则可得命题q：?x∈R，都有x2+x+1＞0为真命题，￢q为假命题
①命题“p∧q”是假命题，故①错误
②命题“￢pⅤq”是真命题，故②正确
③命题“￢pⅤ￢q”为真命题，故③错误
④命题“p∧￢q”是假命题，故④正确
其中正确的命题有②④
故选B
| ||
| 2 |
由于x2+x+1=(x+
| 1 |
| 2 |
| 3 |
| 4 |
①命题“p∧q”是假命题，故①错误
②命题“￢pⅤq”是真命题，故②正确
③命题“￢pⅤ￢q”为真命题，故③错误
④命题“p∧￢q”是假命题，故④正确
其中正确的命题有②④
故选B
点评：本题主要考查了正弦函数的性质及二次函数的性质的应用，简单复合命题的真假关系的判断．
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
（2012•孝感模拟）如图，在A、B间有四个焊接点，若焊接点脱落，而可能导致电路不通，如今发现A、B之间线路不通，则焊接点脱落的不同情况有（ ）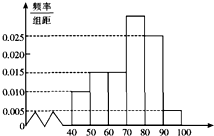
（2012•孝感模拟）某校高一（2）班共有60名同学参加期末考试，现将其数学学科成绩（均为整数）分成六个分数段[40，50），[50，60），…，[90，100]，画出如右图所示的部分频率分布直方图，请观察图形信息，回答下列问题：