题目内容
已知a>0且a≠1,数列{an}是首项与公比均为a的等比数列,数列{bn}满足bn=an•lgan(n∈N*).
(1)若a=2,求数列{bn}的前n项和Sn;
(2)若对于n∈N*,总有bn<bn+1,求a的取值范围.
解:(1)由已知有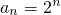 ,
, .…(2分)
.…(2分)
∴ ,
,
∴ ,…(5分)
,…(5分)
所以 ,
,
求得 .…(8分)
.…(8分)
(2)bn<bn+1即nanlga<(n+1)an+1lga.由a>0且a≠1得nlga<(n+1)alga.(2分)
所以 ,或
,或 …(3分)
…(3分)
即 ,或
,或 对任意n∈N*成立,…(5分)
对任意n∈N*成立,…(5分)
而 ,且
,且 ,解得
,解得  或a>1,
或a>1,
即a的取值范围为(0, )∪(1,+∞). …(8分)
)∪(1,+∞). …(8分)
分析:(1)由已知有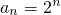 ,
, ,由此可得
,由此可得 ,用错位相减法求出它的值.
,用错位相减法求出它的值.
(2)由条件可得nlga<(n+1)alga,所以 ,或
,或 ,而
,而 ,且
,且 ,由此解得a的取值范围.
,由此解得a的取值范围.
点评:本题主要考查等比数列的定义和性质,等比数列的通项公式,等比数列的前n项和公式的应用,用错位相减法求数列的前n项和.
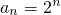 ,
, .…(2分)
.…(2分)∴
 ,
,∴
 ,…(5分)
,…(5分)所以
 ,
,求得
 .…(8分)
.…(8分)(2)bn<bn+1即nanlga<(n+1)an+1lga.由a>0且a≠1得nlga<(n+1)alga.(2分)
所以
 ,或
,或 …(3分)
…(3分)即
 ,或
,或 对任意n∈N*成立,…(5分)
对任意n∈N*成立,…(5分)而
 ,且
,且 ,解得
,解得  或a>1,
或a>1,即a的取值范围为(0,
 )∪(1,+∞). …(8分)
)∪(1,+∞). …(8分)分析:(1)由已知有
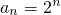 ,
, ,由此可得
,由此可得 ,用错位相减法求出它的值.
,用错位相减法求出它的值.(2)由条件可得nlga<(n+1)alga,所以
 ,或
,或 ,而
,而 ,且
,且 ,由此解得a的取值范围.
,由此解得a的取值范围.点评:本题主要考查等比数列的定义和性质,等比数列的通项公式,等比数列的前n项和公式的应用,用错位相减法求数列的前n项和.

练习册系列答案
相关题目