题目内容
将一块圆心角为
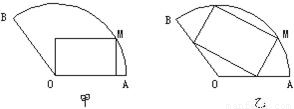
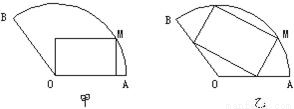
120°,半径为20cm的扇形铁片裁成一块矩形,如图所示,有两种裁法:让矩形一边在扇形的一条半径OA上,或让矩形一边与弦AB平行,试问哪种裁法能得到矩形的面积最大,并求出这个最大值.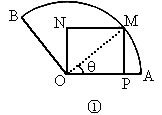
答案:略
解析:
解析:
|
如题图①,要使矩形的面积最大,则 O为某一顶点,且M在 上,设∠MOA=q
(0°<q
<90°),则矩形PM-ON的面积为 上,设∠MOA=q
(0°<q
<90°),则矩形PM-ON的面积为 ,当q
=45时, ,当q
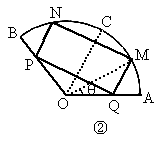
=45时, 的最大值为 的最大值为 .如图②,设∠MOA=q,则∠MQO=120°. .如图②,设∠MOA=q,则∠MQO=120°.
在△ OMQ中,由正弦定理,得 ,由图形的对称性可知, ,由图形的对称性可知,
∠ AOB的平分线OC为对称轴.∴ MN=2OOM·sin(60°-q ).故矩形 PQMN的面积为
当q =30°时,cos(2q -60°)=1时,
 . .
∵  , ,
∴用第二种方法裁得的矩形面积最大,最大面积为  . . |

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目




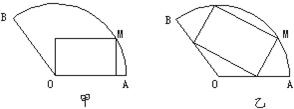 将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.
将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.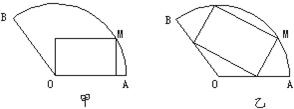 将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.
将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.