题目内容
有四个向量满足 ,
, ,且
,且 ,|
,| |=|
|=| |=1,则
|=1,则 与
与 的夹角=________.
的夹角=________.
0°
分析:由题意知本题根据两个向量垂直,把要求夹角的两个向量联系在一起,要求两个向量的夹角,需要用夹角公式,在夹角公式中模长是已知的,所以只要求出两个向量的数量积就可以求解,利用垂直求出.
解答:∵ ,
,
, ,
, ,
,
∴( )
) =0,
=0,
∴3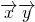 -
- -2
-2 =0,
=0,
∴3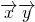 =
=
∵| |=|
|=| |=1,
|=1,
3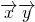 =3,
=3,
∴ ,
,
∴cosθ= =1,
=1,
∵θ∈[0°,180°],
∴θ=0°
故答案为:0°.
点评:本题考查数量积的应用,数量积的主要应用:①求模长;②求夹角;③判垂直,本题是应用中的求夹角,解题过程中注意夹角本身的范围,避免出错.
分析:由题意知本题根据两个向量垂直,把要求夹角的两个向量联系在一起,要求两个向量的夹角,需要用夹角公式,在夹角公式中模长是已知的,所以只要求出两个向量的数量积就可以求解,利用垂直求出.
解答:∵
 ,
,,
 ,
, ,
,∴(
 )
) =0,
=0,∴3
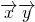 -
- -2
-2 =0,
=0,∴3
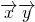 =
=
∵|
 |=|
|=| |=1,
|=1,3
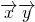 =3,
=3,∴
 ,
,∴cosθ=
 =1,
=1,∵θ∈[0°,180°],
∴θ=0°
故答案为:0°.
点评:本题考查数量积的应用,数量积的主要应用:①求模长;②求夹角;③判垂直,本题是应用中的求夹角,解题过程中注意夹角本身的范围,避免出错.

练习册系列答案
相关题目
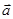 、
、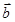 、
、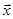 、
、 ,且满足
,且满足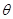 ,求cos
,求cos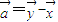 ,
,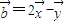 ,且
,且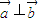 ,|
,|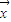 |=|
|=|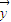 |=1,则
|=1,则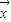 与
与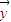 的夹角= .
的夹角= .