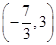题目内容
若关于x的不等式2-x2≥|x-a|至少有一个正数解,则实数a的取值范围是______.
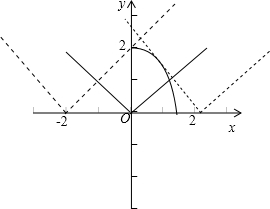
不等式为:2-x2≥|x-a|,且 0≤2-x2.
在同一坐标系画出y=2-x2(y≥0,x>0)和 y=|x|两个函数图象,
将绝对值函数 y=|x|向左移动,当右支经过 (0,2)点,a=-2;
将绝对值函数 y=|x|向右移动让左支与抛物线y=2-x2(y≥0,x>0)相切时,
由
|
再由△=0 解得a=
| 9 |
| 4 |
数形结合可得,实数a的取值范围是(-2,
| 9 |
| 4 |
故答案为:(-2,
| 9 |
| 4 |

练习册系列答案
相关题目
若关于x的不等式2-x2>|x-a|至少有一个负数解,则a的取值范围为( )
A、(-
| ||
B、(-
| ||
C、(-
| ||
D、(-
|
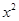 >|x-a|
至少有一个负数解,则实数a的取值范围是
.
>|x-a|
至少有一个负数解,则实数a的取值范围是
.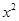 >|x-a| 至少有一个负数解,则a的取值范围为(
)
>|x-a| 至少有一个负数解,则a的取值范围为(
)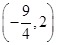 B.
B.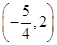 C.
C.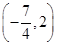 D.
D.