题目内容
已知函数f(x)=ax-lnx(a为常数),
(1)当a=1时,求函数f(x)的最小值;
(2)求函数f(x)在[1,+∞)上的最值;
(3)试证明对任意的n∈N*都有ln(1+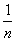 )n<1。
)n<1。
(1)当a=1时,求函数f(x)的最小值;
(2)求函数f(x)在[1,+∞)上的最值;
(3)试证明对任意的n∈N*都有ln(1+
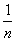 )n<1。
)n<1。 解:(1)当a=1时,函数f(x)=x-lnx,x∈(0,+∞),
∵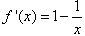 ,
,
令 得x=1,
得x=1,
∵当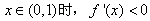 ,
,
∴函数f(x)在(0,1)上为减函数;
∵当 ,
,
∴函数f(x)在(1,+∞)上为增函数,
∴当x=1时,函数f(x)有最小值,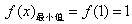 ;
;
(2)∵ ,
,
若a≤0,则对任意的 ,
,
∴函数f(x)在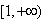 上为减函数,
上为减函数,
∴函数f(x)在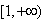 上有最大值,没有最小值,
上有最大值,没有最小值,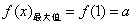 ;
;
若a>0,令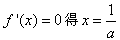 ,
,
当0<a<1时,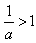 ,
,
当 ,函数f(x)在
,函数f(x)在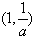 上为减函数;
上为减函数;
当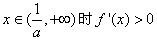 ,∴函数f(x)在
,∴函数f(x)在 上为增函数,
上为增函数,
∴当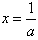 时,函数f(x)有最小值,
时,函数f(x)有最小值,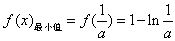 ,
,
当a≥1时, ,在[1,+∞)恒有
,在[1,+∞)恒有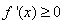 ,
,
∴函数f(x)在[1,+∞)上为增函数,
函数f(x)在[1,+∞)有最小值,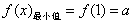 ;
;
综上得:当a≤0时,函数f(x)在[1,+∞)上有最大值, ,没有最小值;
,没有最小值;
当0<a<1时,函数f(x)有最小值, ,没有最大值;
,没有最大值;
当a≥1时,函数f(x)在[1,+∞)有最小值, ,没有最大值。
,没有最大值。
(3)由(1)知函数f(x)=x-lnx在(0,+∞)上有最小值1,
即对任意的x∈(0,+∞)都有 ,
,
当且仅当x=1时“=”成立,
∵n∈N*,
∴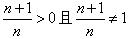 ,
,
∴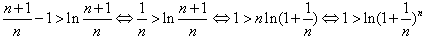 ,
,
∴对任意的n∈N*都有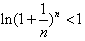 。
。
∵
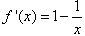 ,
,令
 得x=1,
得x=1,∵当
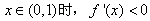 ,
,∴函数f(x)在(0,1)上为减函数;
∵当
 ,
,∴函数f(x)在(1,+∞)上为增函数,
∴当x=1时,函数f(x)有最小值,
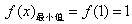 ;
;(2)∵
 ,
,若a≤0,则对任意的
 ,
,∴函数f(x)在
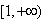 上为减函数,
上为减函数,∴函数f(x)在
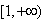 上有最大值,没有最小值,
上有最大值,没有最小值,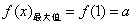 ;
;若a>0,令
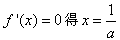 ,
,当0<a<1时,
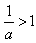 ,
,当
 ,函数f(x)在
,函数f(x)在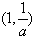 上为减函数;
上为减函数;当
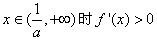 ,∴函数f(x)在
,∴函数f(x)在 上为增函数,
上为增函数,∴当
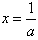 时,函数f(x)有最小值,
时,函数f(x)有最小值,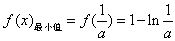 ,
,当a≥1时,
 ,在[1,+∞)恒有
,在[1,+∞)恒有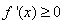 ,
,∴函数f(x)在[1,+∞)上为增函数,
函数f(x)在[1,+∞)有最小值,
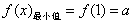 ;
;综上得:当a≤0时,函数f(x)在[1,+∞)上有最大值,
 ,没有最小值;
,没有最小值;当0<a<1时,函数f(x)有最小值,
 ,没有最大值;
,没有最大值;当a≥1时,函数f(x)在[1,+∞)有最小值,
 ,没有最大值。
,没有最大值。(3)由(1)知函数f(x)=x-lnx在(0,+∞)上有最小值1,
即对任意的x∈(0,+∞)都有
 ,
,当且仅当x=1时“=”成立,
∵n∈N*,
∴
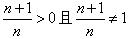 ,
,∴
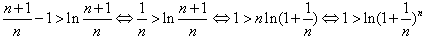 ,
,∴对任意的n∈N*都有
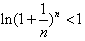 。
。
练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目