题目内容
已知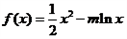 (m
(m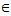 R)
R)
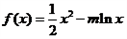 (m
(m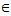 R)
R) (1)若函数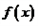 在
在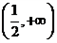 上单调递增,求实数
上单调递增,求实数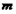 的取值范围;
的取值范围;
(2)当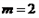 时,求函数
时,求函数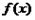 在
在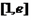 上的最大,最小值。
上的最大,最小值。
(3)求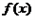 的单调区间。
的单调区间。
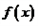 在
在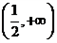 上单调递增,求实数
上单调递增,求实数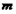 的取值范围;
的取值范围;(2)当
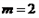 时,求函数
时,求函数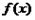 在
在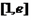 上的最大,最小值。
上的最大,最小值。(3)求
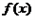 的单调区间。
的单调区间。解:(1) ,
,
若函数 在
在 上单调递增,则
上单调递增,则 在
在 上恒成立,
上恒成立,
即 在
在 上恒成立,
上恒成立,
即 .
.
(2)当 时,
时, ,
,
令 得
得
当 时
时 ,
,
当
 时
时 ,
,
故 是函数
是函数 在
在 上唯一的极小值点,
上唯一的极小值点,
故 .
.
又 ,
, ,
,
故
(3)
当m 0时,
0时, >0对
>0对 恒成立,所以f(x)在
恒成立,所以f(x)在 上调递增。
上调递增。
当m>0时, =0得x=
=0得x= ,0<x<
,0<x< 时,
时, <0,x>
<0,x> 时,
时, >0,
>0,
所以f(x)在 上单调递减,在
上单调递减,在 上调递增。
上调递增。
 ,
,若函数
 在
在 上单调递增,则
上单调递增,则 在
在 上恒成立,
上恒成立,即
 在
在 上恒成立,
上恒成立,即
 .
.(2)当
 时,
时, ,
,令
 得
得
当
 时
时 ,
,当

 时
时 ,
,故
 是函数
是函数 在
在 上唯一的极小值点,
上唯一的极小值点,故
 .
.又
 ,
, ,
,故

(3)

当m
 0时,
0时, >0对
>0对 恒成立,所以f(x)在
恒成立,所以f(x)在 上调递增。
上调递增。当m>0时,
 =0得x=
=0得x= ,0<x<
,0<x< 时,
时, <0,x>
<0,x> 时,
时, >0,
>0,所以f(x)在
 上单调递减,在
上单调递减,在 上调递增。
上调递增。
练习册系列答案
相关题目
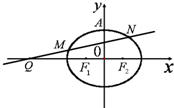 如图,已知椭圆C:
如图,已知椭圆C: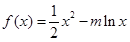 (m
(m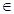 R)
R) 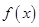 在
在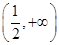 上单调递增,求实数
上单调递增,求实数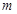 的取值范围;
的取值范围;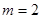 时,求函数
时,求函数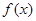 在
在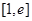 上的最大,最小值;
上的最大,最小值; R上没有极值的概率为
R上没有极值的概率为