题目内容
8.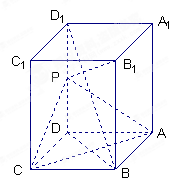 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.(1)求证:直线BD1∥平面PAC;
(2)求证:直线PB1⊥平面PAC.
(3)求三棱锥B-PAC的体积.
分析 (1)直接利用三角形的中位线,得到线线平行,进一步利用线面平行的判定定理得到结论.
(2)利用线面垂直的判定和性质定理和勾股定理得逆定理得到线线垂直,进一步利用线面垂直的判定得到结论.
(3)利用等体积法,求三棱锥B-PAC的体积.
解答 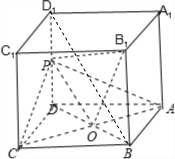 (1)证明:设AC和BD交于点O,连PO,
(1)证明:设AC和BD交于点O,连PO,
由P,O分别是DD1,BD的中点,故PO∥BD1,
所以直线BD1∥平面PAC-------------------------(5分)
(2)证明:PC2=2,PB12=3,B1C2=5,所以△PB1C是直角三角形.
所以PB1⊥PC,----------(8分)
同理PB1⊥PA,所以直线PB1⊥平面PAC.--------(10分)
(3)解:因为P为中点,所以PD=1,易知△ABC为直角三角形,且AB=BC=1,
所以${S_{△ABC}}=\frac{1}{2}AB×BC=\frac{1}{2}⇒{V_{B-PAC}}={V_{P-ABC}}=\frac{1}{3}{S_{△ABC}}×PD=\frac{1}{6}$-----(14分)
点评 本题考查线面平行的判定,线面垂直的判定和性质的应用,考查求三棱锥B-PAC的体积,属于中档题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
20.观察下列各式:

照此规律,当n∈N*时,C2n-10+C2n-11+C2n-12+…+C2n-1n-1=( )

照此规律,当n∈N*时,C2n-10+C2n-11+C2n-12+…+C2n-1n-1=( )
| A. | 4n+1 | B. | 4n | C. | 4n-1 | D. | 4n-2 |
17.已知圆x2+y2=4,直线l:y=x+b,圆上至少有三个点到直线l的距离都是1,则b的取值范围是( )
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | {-$\sqrt{2}$,$\sqrt{2}$} | C. | (-$\sqrt{2}$,$\sqrt{2}$) | D. | [0,$\sqrt{2}$] |
18.在△ABC中,a,b,c分别为角A,B,C所对的边,若(a+b)2-c2=4,且C=60°,则ab的值为( )
| A. | $\frac{4}{3}$ | B. | 1+$\sqrt{3}$ | C. | 1 | D. | $\frac{1+\sqrt{3}}{2}$ |