题目内容
椭圆中有如下结论：椭圆
上斜率为1的弦的中点在直线
上，类比上述结论：双曲线
上斜率为1的弦的中点在直线 上
上斜率为1的弦的中点在直线上，类比上述结论：双曲线上斜率为1的弦的中点在直线 上
试题分析：将椭圆方程
中的
变为
，
变为
，右边变为0，于此得到椭圆上斜率为1的弦的中点在直线
上.类比上述结论，将双曲线的方程作为上述变换可知：双曲线
上斜率为1的弦的中点在直线
.不妨设弦的两个端点为
，
，则
，中点设为
，则
，
，将上述两端点代入双曲线方程得
，两式相减得
，而
，∴
，化简得
，而
，
，于是在直线上.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
的离心率为
，短轴长是2．
时，求k的取值范围．
＋y2＝1上的三个点，O是坐标原点．
+
=1(a>b>0)的左,右焦点分别为F1,F2,点P(a,b)满足|PF2|=|F1F2|.
)2=16相交于M,N两点,且|MN|=
|AB|,求椭圆的方程.
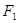的焦点
、
，点
为其上的动点，当∠
，则其离心率为（ ）
+
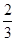
=1(a>b>0)上的任意一点,F1为椭圆的一个焦点,则|PF1|的取值范围为 .
+y2=1截得的最大弦长是( )
