题目内容
【题目】已知向量 ![]() =(cos
=(cos ![]() ,sin
,sin ![]() ),
), ![]() =(cos
=(cos ![]() ,﹣sin
,﹣sin ![]() ),函数f(x)=
),函数f(x)= ![]()
![]() ﹣m|
﹣m| ![]() +
+ ![]() |+1,x∈[﹣
|+1,x∈[﹣ ![]() ,
, ![]() ],m∈R.
],m∈R.
(1)当m=0时,求f( ![]() )的值;
)的值;
(2)若f(x)的最小值为﹣1,求实数m的值;
(3)是否存在实数m,使函数g(x)=f(x)+ ![]() m2 , x∈[﹣
m2 , x∈[﹣ ![]() ,
, ![]() ]有四个不同的零点?若存在,求出m的取值范围;若不存在,说明理由.
]有四个不同的零点?若存在,求出m的取值范围;若不存在,说明理由.
【答案】
(1)解: ![]()
![]() =(cos
=(cos ![]() ,sin
,sin ![]() )(cos
)(cos ![]() ,﹣sin
,﹣sin ![]() )=cos
)=cos ![]() cos
cos ![]() ﹣sin
﹣sin ![]() sin
sin ![]() =cos(
=cos( ![]() +
+ ![]() )=cos2x,
)=cos2x,
当m=0时,f(x)= ![]()
![]() +1=cos2x+1,
+1=cos2x+1,
则f( ![]() )=cos(2×
)=cos(2× ![]() )+1=cos
)+1=cos ![]() +1=
+1= ![]() ;
;
(2)解:∵x∈[﹣ ![]() ,
, ![]() ],
],
∴| ![]() +
+ ![]() |=
|= ![]() =
= ![]() =2cosx,
=2cosx,
则f(x)= ![]()
![]() ﹣m|
﹣m| ![]() +
+ ![]() |+1=cos2x﹣2mcosx+1=2cos2x﹣2mcosx,
|+1=cos2x﹣2mcosx+1=2cos2x﹣2mcosx,
令t=cosx,则 ![]() ≤t≤1,
≤t≤1,
则y=2t2﹣2mt,对称轴t= ![]() ,
,
①当 ![]() <
< ![]() ,即m<1时,
,即m<1时,
当t= ![]() 时,函数取得最小值此时最小值y=
时,函数取得最小值此时最小值y= ![]() ﹣m=﹣1,得m=
﹣m=﹣1,得m= ![]() (舍),
(舍),
②当 ![]() ≤
≤ ![]() ≤1,即m<1时,
≤1,即m<1时,
当t= ![]() 时,函数取得最小值此时最小值y=﹣
时,函数取得最小值此时最小值y=﹣ ![]() =﹣1,得m=
=﹣1,得m= ![]() ,
,
③当 ![]() >1,即m>2时,
>1,即m>2时,
当t=1时,函数取得最小值此时最小值y=2﹣2m=﹣1,得m= ![]() (舍),
(舍),
综上若f(x)的最小值为﹣1,则实数m= ![]() .
.
(3)解:令g(x)=2cos2x﹣2mcosx+ ![]() m2=0,得cosx=
m2=0,得cosx= ![]() 或
或 ![]() ,
,
∴方程cosx= ![]() 或
或 ![]() 在x∈[﹣
在x∈[﹣ ![]() ,
, ![]() ]上有四个不同的实根,
]上有四个不同的实根,
则 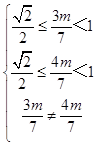 ,得
,得 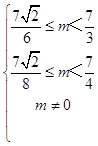 ,则
,则 ![]() ≤m<
≤m< ![]() ,
,
即实数m的取值范围是 ![]() ≤m<
≤m< ![]() .
.
【解析】(1)利用向量数量积的公式化简函数f(x)即可.(2)求出函数f(x)的表达式,利用换元法结合一元二次函数的最值性质进行讨论求解即可.(3)由g(x)=0得到方程的根,利用三角函数的性质进行求解即可.

 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案