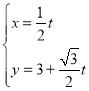Question

【题目】已知过点且离心率为的椭圆的中心在原点，焦点在轴上．

（1）求椭圆的方程；

（2）设点是椭圆的左准线与轴的交点，过点的直线与椭圆相交于两点，记椭圆的左，右焦点分别为，上下两个顶点分别为.当线段的中点落在四边形内（包括边界）时，求直线斜率的取值范围．

Answer 1

【答案】（1）；（2）

【解析】

试题分析：（1）设椭圆的方程，用待定系数法求出的值；（2）解决直线和椭圆的综合问题时需注意：第一步，根据题意设直线方程，有的题设条件已知点，而斜率未知；有的题设条件已知斜率，点不定，可由点斜式设直线方程.第二步，联立方程，把所设直线方程与椭圆的方程联立，消去一个元，得到一个一元二次方程.第三步，求解判别式，计算一元二次方程根.第四步，根据题设条件求解问题中结论.

试题解析：（1）依题意，设椭圆的方程为（）,焦距为，

由题设条件知，，即，所以，由椭圆过点，则有，解得，，故椭圆的方程为．·······7分

（2）椭圆的左准线方程为,所以点的坐标为（-4,0），

显然直线的斜率存在，所以直线的方程为．

设点的坐标分别为，线段的

中点为，

由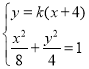

得 ， ① ·······9分

由，

解得 ， ② ·······11分

因为是方程①的两根，所以，

于是， ·······12分

∵，所以点不可能在轴的右边．

又直线方程分别为，

所以点在正方形内（包括边界）的充要条件为

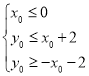，即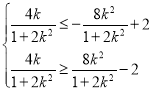 ·······14分

解得，此时②也成立．故直线斜率的取值范围是． ······16分