题目内容
如图，已知四棱锥P-ABCD的底面积是菱形，AC交BD于O，PO⊥平面ABC，E为AD中点，F在PA上，AP=λAF，PC∥平面BEF．
（1）求λ的值；
（2）若2，∠ADB=∠BPC=60°，求二面角B-AF-E的余弦值．
分析：（1）设AO交BE于G，连接FG，由O、E分别是BD、AD的中点，知
=
，
=
，由此能求出λ的值．
（2）以OA为x轴，以OB为y轴，以OP为z轴，建立空间直角坐标系，利用向量法能够求出二面角B-AF-E的余弦值．
| AG |
| AO |
| 2 |
| 3 |
| AG |
| AC |
| 1 |
| 3 |
（2）以OA为x轴，以OB为y轴，以OP为z轴，建立空间直角坐标系，利用向量法能够求出二面角B-AF-E的余弦值．
解答：解：（1）设AO交BE于G，连接FG，
∵O、E分别是BD、AD的中点，
∴
=
，
=
，
∵PC∥平面BEF，∴GF∥PC，
∴
=
=
，∴λ=
．
（2）以OA为x轴，以OB为y轴，以OP为z轴，建立如图所示的空间直角坐标系，
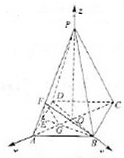
设OB=1，在菱形ABCD中，∵∠ADB=60°，
∴△ABD是等边三角形，故OA=
，
∵∠BPD=60°，PO⊥平面ABC，
∴PO=
，
∴A（
，0，0），B（0，1，0），P（0，0，
），D（0，-1，0），
∴
=（-
，-1，0），
=（-
，0，
），
=（-
，1，0），
设平面PAD的法向量为
=（x1，y1，z1），则
•
=0，
•
=0，
∴
，∴
=(-
，3，-
)，
设平面PAB的法向量为
=(x2，y2，z2)，则
•
=0，
•
=0，
∴
，∴
=(
，3，
)，
设二面角B-AF-E的平面角为θ，
则cosθ=|cos＜
，
＞|=|
|=
．
∴二面角B-AF-E的余弦值是
．
∵O、E分别是BD、AD的中点，
∴
| AG |
| AO |
| 2 |
| 3 |
| AG |
| AC |
| 1 |
| 3 |
∵PC∥平面BEF，∴GF∥PC，
∴
| AE |
| AP |
| AG |
| AC |
| 1 |
| 3 |
| 1 |
| 3 |
（2）以OA为x轴，以OB为y轴，以OP为z轴，建立如图所示的空间直角坐标系，
设OB=1，在菱形ABCD中，∵∠ADB=60°，
∴△ABD是等边三角形，故OA=
| 3 |
∵∠BPD=60°，PO⊥平面ABC，
∴PO=
| 3 |
∴A（
| 3 |
| 3 |
∴
| AD |
| 3 |
| AP |
| 3 |
| 3 |
| AB |
| 3 |
设平面PAD的法向量为
| m |
| m |
| AD |
| m |
| AP |
∴
|
| m |
| 3 |
| 3 |
设平面PAB的法向量为
| n |
| n |
| AP |
| n |
| AB |
∴
|
| n |
| 3 |
| 3 |
设二面角B-AF-E的平面角为θ，
则cosθ=|cos＜
| m |
| n |
| -3+9-3 | ||||
|
| 1 |
| 5 |
∴二面角B-AF-E的余弦值是
| 1 |
| 5 |
点评：本题考查二面角的余弦值的求法，解题时要认真审题，仔细解答，注意向量法和等价转化思想的合理运用．
练习册系列答案
相关题目
如图：已知四棱锥P-ABCD中，PD⊥平面ABCD，ABCD是正方形，E是PA的中点，
如图，已知四棱锥P-ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
如图，已知四棱锥P-ABCD的底面为菱形，∠BCD=60°，PD⊥AD．点E是BC边上的中点．
（2012•崇明县二模）如图，已知四棱锥P-ABCD的底面ABCD为正方形，PA⊥平面ABCD，E、F分别是BC，PC的中点，AB=2，AP=2．
（2012•吉林二模）如图，已知四棱锥P-ABCD的底面是正方形，PA⊥面ABCD，且PA=AD=2，点M，N分别在PD，PC上，