题目内容
若函数f(x)=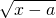 的反函数为y=f-1(x),且f-1(2)=1,则f (2)=______
的反函数为y=f-1(x),且f-1(2)=1,则f (2)=______
解:法一:由已知设y=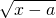 并解x得:x=y2+a
并解x得:x=y2+a
∴函数f(x)=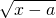 的反函数为f-1(x)=x2+a,
的反函数为f-1(x)=x2+a,
由f-1(2)=1得:4+a=1,即:a=-3
∴f(x)=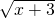 ,从而,f (2)=
,从而,f (2)= ;
;
法二:∵f-1(2)=1,∴f(1)=2
由此得: ,∴a=-3
,∴a=-3
∴f(x)=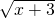 ,从而,f (2)=
,从而,f (2)= ;
;
答案:
分析:本题考查反函数的概念、反函数的求法、互为反函数的函数图象之间的关系、等相关知识;
可以用两种方法:
其一、求出反函数,将f-1(2)=1代入求出a的值,然后f (2)可求;
其二、利用互为反函数的函数图象关于y=x对称这一特征,将f-1(2)=1转化为f(1)=2,直接代入原函数求a.
点评:本题方法二的解答,巧妙的利用了原函数和反函数的关系,将f-1(2)=1转化为f(1)=2,直接代入原函数求a,回避了求反函数的过程.过程简捷,计算简单,这要比方法一求出反函数,再将点的坐标代入方便得多.
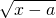 并解x得:x=y2+a
并解x得:x=y2+a∴函数f(x)=
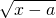 的反函数为f-1(x)=x2+a,
的反函数为f-1(x)=x2+a,由f-1(2)=1得:4+a=1,即:a=-3
∴f(x)=
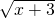 ,从而,f (2)=
,从而,f (2)= ;
;法二:∵f-1(2)=1,∴f(1)=2
由此得:
 ,∴a=-3
,∴a=-3∴f(x)=
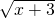 ,从而,f (2)=
,从而,f (2)= ;
;答案:

分析:本题考查反函数的概念、反函数的求法、互为反函数的函数图象之间的关系、等相关知识;
可以用两种方法:
其一、求出反函数,将f-1(2)=1代入求出a的值,然后f (2)可求;
其二、利用互为反函数的函数图象关于y=x对称这一特征,将f-1(2)=1转化为f(1)=2,直接代入原函数求a.
点评:本题方法二的解答,巧妙的利用了原函数和反函数的关系,将f-1(2)=1转化为f(1)=2,直接代入原函数求a,回避了求反函数的过程.过程简捷,计算简单,这要比方法一求出反函数,再将点的坐标代入方便得多.

练习册系列答案
相关题目