题目内容
函数  零点的个数( )
零点的个数( )
| A.不存在 | B.有一个 | C.有两个 | D.有三个 |
D
解析试题分析:依题意, ,因为
,因为 ,易知当
,易知当 ,
, .
.  ,
, ,
, ,且根据指数函数与幂函数的增长趋势知,当
,且根据指数函数与幂函数的增长趋势知,当 时,
时, .所以函数
.所以函数 在
在 上单调递减,在
上单调递减,在 上单调递增,在
上单调递增,在 单调递减.即函数
单调递减.即函数 在定义域上先减后增再减的趋势.又知
在定义域上先减后增再减的趋势.又知 ,
, ,
, ,
, .所以函数
.所以函数 在
在 、
、 、
、 上各有一个零点,即函数
上各有一个零点,即函数  零点的个数为3个.
零点的个数为3个.
考点:函数的零点

练习册系列答案
相关题目
函数 的零点个数为( )
的零点个数为( )
| A.1 | B.2 | C.3 | D.4 |
设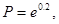
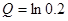 ,
,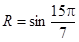 ,则( )
,则( )
A.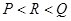 | B.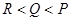 | C.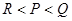 | D.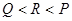 |
已知 ,则
,则 ( )
( )
A. | B. | C. | D. |
设 ,且
,且 ,则
,则 = ( )
= ( )
| A.100 | B.20 | C.10 | D. |
某家具的标价为132元,若降价以九折出售(即优惠10%),仍可获利10%(相对进货价),则该家具的进货价是( )
| A.118元 | B. 105元 | C. 106元 | D. 108元 |
设函数 ,若
,若 则
则 ( )
( )
A. | B.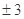 | C.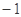 | D. |
设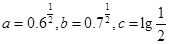 ,则
,则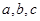 之间的关系是 ( )
之间的关系是 ( )
A.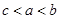 | B.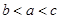 | C.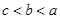 | D.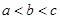 |
 的一个根所在的区间是( )
的一个根所在的区间是( )

