Question

设函数f（x）=x²-aln（x+1），其中a∈R．
（Ⅰ）若f'（1）=0，求a的值；
（Ⅱ）当a＜0时，讨论函数f（x）在其定义域上的单调性；
（Ⅲ）证明：对任意的正整数n，不等式ln(n+1)＞

n

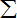k=1

(

1

k2

-

1

k3

)都成立．

Answer 1

（Ⅰ）求导函数，可得f′(x)=2x-

a

x+1

∵f′（1）=0，∴2-

a

2

=0，∴a=4；
（Ⅱ）当a＜0时，令f′（x）＜0可得-1＜x＜

-1+ 1-2a

2

，令f′（x）＞0可得x＞

-1+ 1-2a

2

，
∴当a＜0时，函数的单调减区间是（-1，

-1+ 1-2a

2

），单调增区间是（

-1+ 1-2a

2

，+∞）；
（Ⅲ）证明：令g（x）=x²-ln（x+1）-x³（0＜x≤1），
则g′（x）=

-3x3-(x-1)2

x+1

，当0＜x≤1时，g'（x）＜0，
∴g（x）在（0，1]上为减函数，
∴g（x）＜g（0）=0，
∴x²-ln（x+1）-x³＜0
∴ln（x+1）＞x²-x³，
令x=

1

n

，则ln(1+

1

n

)＞

1

n2

-

1

n3

，∴ln(n+1)-lnn＞

1

n2

-

1

n3

∴

n

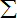k=1

(

1

k2

-

1

k3

)＜ln2-ln1+ln3-ln2+…+ln（n+1）-lnn=ln（n+1）
∴不等式ln(n+1)＞

n

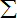k=1

(

1

k2

-

1

k3

)都成立．