Question

已知椭圆

x2

2

+

y2

1

=1的左，右焦点分别为F₁，F₂，若过点P（0，-2）及F₁的直线交椭圆于A，B两点，则△ABF₂的周长为

4

2

，△ABF₂的面积为

4 10

9

．

Answer 1

分析：利用椭圆的定义即可得到△ABF₂的周长；把直线AB的方程与椭圆方程联立得到根与系数的关系，再利用弦长公式、点到直线的距离公式、三角形的面积公式即可得出．

解答：解：如图所示，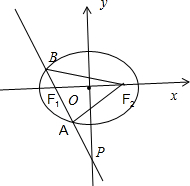
①由椭圆

x2

2

+

y2

1

=1得a²=2，b=1，c=

a2-b2

=1．得F₁（-1，0），F₂（1，0）．
∴|AF₁|+|AF₂|=|BF₁|+|BF₂|=2a=2

2

．
∴△ABF₂的周长=|AB|+|AF₂|+|BF₂|=4a=4

2

．
②直线PF₁的方程为y=

0-(-2)

-1-0

x-2，即y=-2x-2．
设A（x₁，y₁），B（x₂，y₂）．
联立

y=-2x-2 x2+2y2=2

，化为9x²+16x+6=0，
∴x1+x2=-

16

9

，x1x2=

2

3

．
∴|AB|=

(1+22)[(x1+x2)2-4x1x2]

=

5×[( 16 9 )2-4× 2 3 ]

=

10 2

9

．
点F₂到直线AB的距离d=

4

5

．
∴S△ABF2=

1

2

|AB|•d=

1

2

×

10 2

3

×

4

5

=

4 10

9

．
故答案分别为4

2

；  

4 10

9

．

点评：熟练掌握椭圆的定义、直线与椭圆相交问题转化为方程联立得到根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积公式等是解题的关键．