题目内容
设F1、F2分别为椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(1)若椭圆C上的点A(1,
| 3 |
| 2 |
(2)设点K是(1)中所得椭圆上的动点,求线段F1K的中点的轨迹方程.
分析:(1)把已知点的坐标代入椭圆方程,再由椭圆的定义知2a=4,从而求出椭圆的方程,由椭圆的方程求出焦点坐标.
(2)设F1K的中点Q(x,y),则由中点坐标公式得点K(2x+1,2y),把K的坐标代入椭圆方程,化简即得线段KF1的中点Q的轨迹方程.
(2)设F1K的中点Q(x,y),则由中点坐标公式得点K(2x+1,2y),把K的坐标代入椭圆方程,化简即得线段KF1的中点Q的轨迹方程.
解答:解:(1)椭圆C的焦点在x轴上,由椭圆上的点A到F1、F2两点的距离之和是4,得2a=4,即a=2.…(2分)
又点A(1,
)在椭圆上,因此
+
=1得b2=3,于是c2=1.…(4分)
所以椭圆C的方程为
+
=1,…(5分)
焦点F1(-1,0),F2(1,0).…(7分)
(2)设椭圆C上的动点为K(x1,y1),线段F1K的中点Q(x,y)满足:x=
,y=
,即x1=2x+1,y1=2y.…(11分)
因此
+
=1.即(x+
)2+
=1为所求的轨迹方程.…(15分)
又点A(1,
| 3 |
| 2 |
| 1 |
| 22 |
(
| ||
| b2 |
所以椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
焦点F1(-1,0),F2(1,0).…(7分)
(2)设椭圆C上的动点为K(x1,y1),线段F1K的中点Q(x,y)满足:x=
| -1+x1 |
| 2 |
| y1 |
| 2 |
因此
| (2x+1)2 |
| 4 |
| (2y)2 |
| 3 |
| 1 |
| 2 |
| 4y2 |
| 3 |
点评:本题考查椭圆的简单性质、线段的中点公式,以及用代入法求轨迹方程.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 (a>b>0)的左、右两个焦点,椭圆C上的点
(a>b>0)的左、右两个焦点,椭圆C上的点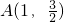 到两点的距离之和等于4.
到两点的距离之和等于4. 求|PQ|的最大值.
求|PQ|的最大值.