题目内容
21.已知函数f(x)=|x-a|,g(x)=x2+2ax+1(a为正常数),且函数f(x)与g(x)的图象在y轴上的截距相等.(1)求a的值;
(2)求函数f(x)+g(x)的单调递增区间;
(3)若n为正整数,证明:10f(n)·(![]() )g(n)<4.
)g(n)<4.
21.[解](1)由题意,f(0)=g(0),|a|=1,又a>0,∴a=1.
(2)f(x)+g(x)=|x-1|+x2+2x+1,
当x≥1时,f(x)+g(x)=x2+3x,它在[1,+∞]上单调递增;
当x<1时,f(x)+g(x)=x2+x+2,它在[-![]() ,1]上单调递增.
,1]上单调递增.
因此,函数f(x)+g(x)的单调递增区间为[-![]() ,+∞]. [证法一](3)设cn=10f(n)·(
,+∞]. [证法一](3)设cn=10f(n)·(![]() )g(n),考查数列{cn}的变化规律.
)g(n),考查数列{cn}的变化规律.
解不等式![]() <1,由cn>0,上式化为10·(
<1,由cn>0,上式化为10·(![]() )
)![]() <1,
<1,
解得n>-![]() -
-![]() ≈3.7,
≈3.7,
∵n是正整数,得n≥4,
于是c1≤c2≤c3≤c4,而c4>c5>…,
∴10f(n)·(![]() )
)![]() ≤103·(
≤103·(![]() )
)![]() <4. [证法二](3)10
<4. [证法二](3)10![]() ·(
·(![]() )
)![]() =10
=10![]() ·(
·(![]() )
)![]() ,考查
,考查
lg![]() =(n-1)+(n+1)2lg
=(n-1)+(n+1)2lg![]() =(lg
=(lg![]() )n2+(1+2lg
)n2+(1+2lg![]() )n+
)n+
(-1+lg![]() )
)
∵lg![]() <0,当x=-
<0,当x=-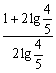 ≈4.2时,
≈4.2时,
函数(lg![]() )x2+(1+2lg
)x2+(1+2lg![]() )x+(-1+lg
)x+(-1+lg![]() )达到最大值.
)达到最大值.
∴若n为正整数时,则当n=4时,lg![]() 达到最大值.于是,lg
达到最大值.于是,lg![]() ≤lg
≤lg![]() <0.6,
<0.6,
而lg4>0.6,∴lg 即10(n-1)·(![]()
![]() )
)![]() <4.
<4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有