Question

若上是减函数，则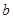的取值范围是    __.

Answer 1

解析试题分析：∵f′(x)=-x+
∵f（x）在区间（-1，+∞）上是减函数，
∴f′(x)=-x+≤0在区间（-1，+∞）上恒成立
∴b≤x²+2x在区间（1，+∞）上恒成立
∵x²+2x=＞-1∴．
考点：本题主要考查应用导数研究函数的单调性及最值。
点评：典型题，此类题目属于导数的基本应用问题，本题将函数在某区间是减函数，转化成不等式恒成立问题，通过求函数的最值，达到解题目的，是一般解法。