题目内容
(本小题满分14分)已知定义域为R的函数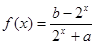 是奇函数.
是奇函数.
(1)求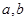 的值;
的值;
(2)用定义证明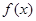 在
在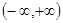
 上为减函数.
上为减函数.
(3)若对于任意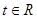 ,不等式
,不等式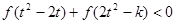 恒成立,求
恒成立,求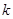 的范围.
的范围.
【答案】
(1) 符合题意. (2)见解析; (3)
符合题意. (2)见解析; (3)
【解析】本试题主要是考查了函数的奇偶性以及单调性和不等式的求解的综合运用。
(1)
又 ,得
,得
(2)因为任取 (4分)
(4分)
则 =
=
作差,得到函数 单调性,进而证明。
(3)
 ,不等式
,不等式 恒成立,
恒成立,
 利用单调性求解。
利用单调性求解。
解:
(1)
又 ,得
,得 (2分) 经检验
(2分) 经检验 符合题意.(3分)
符合题意.(3分)
(2)任取 (4分)
(4分)
则 =
=
= (6分)
(6分)
 (8分)
(8分)
(3)
 ,不等式
,不等式 恒成立,
恒成立,

 为奇函数,
为奇函数,  (10分)
(10分)
 为减函数,
为减函数,  (11分)
(11分)
即 恒成立,而
恒成立,而 (13分)
(13分)
 (14分)
(14分)

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)