题目内容
已知椭圆C的中心在原点,焦点在x轴上,一条经过点(3,-(1)求直线l的方程;
(2)求椭圆C长轴长的取值范围.
解:(1)直线l过点(3,-![]() ),且方向向量a=(-2,
),且方向向量a=(-2,![]() ),
),
∴l的方程为![]() =
=![]() ,即y=-
,即y=-![]() (x-1).
(x-1).
(2)设直线y=-![]() (x-1)和椭圆
(x-1)和椭圆![]() +
+![]() =1交于两点A(x1,y1)、B(x2,y2),和x轴交于点M(1,0),
=1交于两点A(x1,y1)、B(x2,y2),和x轴交于点M(1,0),
由![]() =2
=2![]() ,知y1=-2y2.
,知y1=-2y2.
将x=-![]() y+1代入b2x2+a2y2=a2b2中,得(
y+1代入b2x2+a2y2=a2b2中,得(![]() b2+a2)y2-
b2+a2)y2-![]() b2y+b2(1-a2)=0.
b2y+b2(1-a2)=0.
由韦达定理有
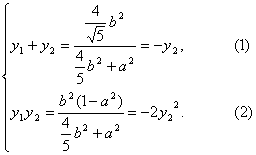
∵有两交点,
∴Δ=(![]() b2)2-4(
b2)2-4(![]() b2+a2)·b2(1-a2)>0,
b2+a2)·b2(1-a2)>0,
化简得5a2+4b2>5. (3)
由(1)(2)消去y2,得32b2=(4b2+5a2)(a2-1),
即4b2=![]() >0. (4)
>0. (4)
将(4)代入(3),得5a2+![]() >5. (5)
>5. (5)
可求得1<a2<9.
又椭圆的焦点在x轴上,则a2>b2.
∴4b2=![]() <4a2.
<4a2.
综上,得1<a2<![]() ;可解得1<a<
;可解得1<a<![]() .
.
∴所求椭圆长轴长2a的范围是(2,![]() ).
).

练习册系列答案
相关题目

 。
。