题目内容
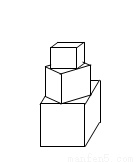
 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是
- A.4
- B.5
- C.6
- D.7
C
分析:求出各个层的正方体的表面积,求出它们的和,该塔形的表面积(含最底层正方体的底面面积)超过39,求出正方体的个数至少个数.
解答:底层正方体的表面积为24;第2层正方体的棱长 ,每个面的面积为
,每个面的面积为 ;第3层正方体的棱长为
;第3层正方体的棱长为 ,每个面的面积为
,每个面的面积为 ;┉,第n层正方体的棱长为
;┉,第n层正方体的棱长为 ,每个面的面积为
,每个面的面积为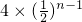 ;
;
若该塔形为n层,则它的表面积为
24+4[ +
+ +┉+
+┉+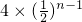 ]=40
]=40
因为该塔形的表面积超过39,所以该塔形中正方体的个数至少是6.
故选C
点评:本题是中档题,考查计算能力,数列求和的知识,正确就是解好数学问题的关键,常考题型.
分析:求出各个层的正方体的表面积,求出它们的和,该塔形的表面积(含最底层正方体的底面面积)超过39,求出正方体的个数至少个数.
解答:底层正方体的表面积为24;第2层正方体的棱长
 ,每个面的面积为
,每个面的面积为 ;第3层正方体的棱长为
;第3层正方体的棱长为 ,每个面的面积为
,每个面的面积为 ;┉,第n层正方体的棱长为
;┉,第n层正方体的棱长为 ,每个面的面积为
,每个面的面积为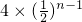 ;
;若该塔形为n层,则它的表面积为
24+4[
 +
+ +┉+
+┉+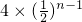 ]=40
]=40
因为该塔形的表面积超过39,所以该塔形中正方体的个数至少是6.
故选C
点评:本题是中档题,考查计算能力,数列求和的知识,正确就是解好数学问题的关键,常考题型.

练习册系列答案
相关题目
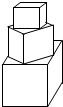 有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( )
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( )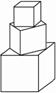
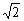
 A 4;
A 4;