题目内容
已知函数![]() ,
,
(1)判断函数![]() 的奇偶性;
的奇偶性;
(2)求函数![]() 的单调区间;
的单调区间;
(3)若关于![]() 的方程
的方程![]() 有实数解,求实数
有实数解,求实数![]() 的取值范围.
的取值范围.
解:(1)函数![]() 的定义域为
的定义域为![]() 且
且![]() .--------------- 1分
.--------------- 1分
![]()
![]() 为偶函数.--------------- 3分
为偶函数.--------------- 3分
(2)当![]() 时,
时,![]() --------------- 4分
--------------- 4分
令![]()
![]()
![]()
![]()
令![]()
![]()
![]()
![]()
所以可知:当![]() 时,
时,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() 单调递增,---------- 6分
单调递增,---------- 6分
又因为![]() 是偶函数,所以在对称区间上单调性相反,所以可得:
是偶函数,所以在对称区间上单调性相反,所以可得:
当![]() 时,
时,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() 单调递减,
单调递减,
综上可得:![]() 的递增区间是:
的递增区间是:![]() ,
,![]() ;
;
![]() 的递减区间是:
的递减区间是: ![]() ,
,![]() --------------------------- 8分
--------------------------- 8分
(3)由![]() ,即
,即![]() ,显然,
,显然,![]()
可得:![]() --------------------- 9分
--------------------- 9分
令![]() ,当
,当![]() 时,
时,![]()
![]()
![]()
![]() ----------- 10分
----------- 10分
显然![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
![]() 时,
时, ![]() ----------- 12分
----------- 12分
又![]() ,所以可得
,所以可得![]() 为奇函数,所以
为奇函数,所以![]() 图像关于坐标原点对称
图像关于坐标原点对称
所以可得:当![]() 时,
时,![]() ----------- 13分
----------- 13分
∴![]() 的值域为
的值域为![]() ∴
∴![]() 的取值范围是
的取值范围是![]() .-------- 14分
.-------- 14分

练习册系列答案
相关题目

 (理)已知函数
(理)已知函数
 ,有h(h(a))=a;
,有h(h(a))=a;
 ,使得h(m)=m,若m是函数h(x)的中介元,记
,使得h(m)=m,若m是函数h(x)的中介元,记 时h(x)的中介元为xn,且
时h(x)的中介元为xn,且 ,若对任意的
,若对任意的 ,都有Sn<
,都有Sn<  ,求
,求 的取值范围;
的取值范围; 时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
时,函数y= h(x)的图像总在直线y=1-x的上方,求P的取值范围。
 (理)已知函数
(理)已知函数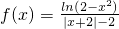 .
.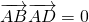 ,求D2+E2-4F的值;
,求D2+E2-4F的值; .
. ,求D2+E2-4F的值;
,求D2+E2-4F的值;
