题目内容
已知函数f(x)=sin(π﹣ωx)cosωx+cos2ωx(ω>0)的最小正周期为π.
(Ⅰ)求ω的值;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短到原来的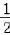 ,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间
,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间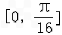 上的最小值.
上的最小值.
(Ⅰ)求ω的值;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短到原来的
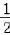 ,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间
,纵坐标不变,得到函数y=g(x)的图象,求函数y=g(x)在区间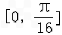 上的最小值.
上的最小值. 解:(Ⅰ)∵f(x)=sin(π﹣ωx)cosωx+cos2ωx,
∴f(x)=sinωxcosωx+ +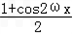
= sin2ωx+
sin2ωx+ cos2ωx+
cos2ωx+
=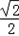 sin(2ωx+
sin(2ωx+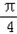 )+
)+
由于ω>0,依题意得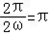 ,所以ω=1;
,所以ω=1;
(Ⅱ)由(Ⅰ)知f(x)=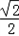 sin(2x+
sin(2x+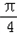 )+
)+ ,
,
∴g(x)=f(2x)=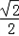 sin(4x+
sin(4x+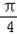 )+
)+
∵0≤x≤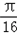 时,
时,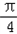 ≤4x+
≤4x+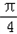 ≤
≤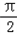 ,
,
∴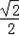 ≤sin(4x+
≤sin(4x+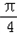 )≤1,
)≤1,
∴1≤g(x)≤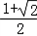 ,
,
∴f(x)=sinωxcosωx+ +
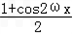
=
 sin2ωx+
sin2ωx+ cos2ωx+
cos2ωx+
=
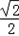 sin(2ωx+
sin(2ωx+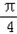 )+
)+
由于ω>0,依题意得
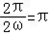 ,所以ω=1;
,所以ω=1;(Ⅱ)由(Ⅰ)知f(x)=
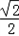 sin(2x+
sin(2x+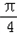 )+
)+ ,
,∴g(x)=f(2x)=
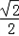 sin(4x+
sin(4x+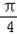 )+
)+
∵0≤x≤
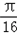 时,
时,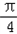 ≤4x+
≤4x+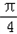 ≤
≤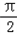 ,
,∴
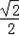 ≤sin(4x+
≤sin(4x+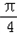 )≤1,
)≤1,∴1≤g(x)≤
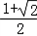 ,
,
练习册系列答案
相关题目
