题目内容
若sin(α+β)cosβ-cos(α+β)sinβ=0,则sin(α+2β)+sin(α-2β)等于( )A.1 B.-1 C.0 D.±1
解析:由sin(α+β)cosβ-cos(α+β)sinβ=0,
可得sin[(α+β)-β]=sinα=0,而sin(α+2β)+sin(α-2β)
=(sinαcos2β+cosαsin2β)+(sinαcos2β-cosαsin2β)=2sinαcos2β=0.
答案:C

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
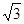 ,且c =
,且c =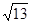 ,C =
,C =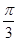 ,求a,b的值
,求a,b的值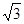 ,且c =
,且c =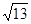 ,C =
,C =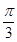 ,求a,b的值.
,求a,b的值.  .
. ,试判断△ABC的形状并说明理由
,试判断△ABC的形状并说明理由 .
. ,试判断△ABC的形状并说明理由
,试判断△ABC的形状并说明理由