Question

已知α，β是三次函数f(x)=

1

3

x3+

1

2

ax2+2bx(a，b∈R)的两个极值点，且α∈（0，1），β∈（1，2），求动点（a，b）所在区域面积S．

Answer 1

分析：已知α，β是三次函数f(x)=

1

3

x3+

1

2

ax2+2bx(a，b∈R)的两个极值点，对f（x）进行求导，可知α，β是方程x²+ax+2b=0的两个根，根据α∈（0，1），β∈（1，2），求出可行域，利用数形结合的方法进行求解；

解答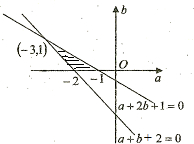：解：由函数f(x)=

1

3

x3+

1

2

ax2+2bx(a，b∈R)可得，
f'（x）=x²+ax+2b，…（2分）
由题意知，α，β是方程x²+ax+2b=0的两个根，…（5分）
且α∈（0，1），β∈（1，2），
因此得到可行域

f′(0)=2b＞0 f′(1)=1+a+26＜0 f′(2)=4+2a+2b＞0

…（9分）
即

b＞0 a+2b+1＜0 a+b+2＞0

，画出可行域如图．…（11分）
所以S=

1

2

×1×1=

1

2

…（12分）；

点评：此题是一道简单的线性规划问题，利用导数研究函数的单调性，根据二次函数根与系数的关系得出可行域，此题是一道基础题；